Dẫn V(lít) khí CO2 vào V(ml) dung dịch Ca(OH)2 2M(dư) thu được 30g kết tủa.
a, tính VCO2
b, tính thể tích dung dịch Ca(OH)2 tối thiểu cần dùng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 10 2023
\(a.n_{CO_2}=\dfrac{0,672}{22,4}=0,03mol\\ CO_2+Ca\left(OH\right)_2\rightarrow CaCO_3+H_2O\)
\(n_{CO_2}=n_{Ca\left(OH\right)_2}=n_{CaCO_3}=0,03mol\\ m_{CaCO_3}=0,03.100=3g\\ b.V_{ddCa\left(OH\right)_2}=\dfrac{0,03}{1,5}=0,02l\)
16 tháng 3 2023
a, \(C_2H_4+Br_2\rightarrow C_2H_4Br_2\)
\(C_2H_2+2Br_2\rightarrow C_2H_2Br_4\)
b, \(n_{C_2H_4}+n_{C_2H_2}=\dfrac{0,56}{22,4}=0,025\left(mol\right)\left(1\right)\)
Theo PT: \(n_{Br_2}=n_{C_2H_4}+2n_{C_2H_2}=\dfrac{2,8}{160}=0,0175\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{C_2H_4}=0,0325\left(mol\right)\\n_{C_2H_2}=-0,0075\end{matrix}\right.\)
Đến đây thì ra số mol âm, bạn xem lại đề nhé.
11 tháng 10 2023
\(a/n_{CO_2}=\dfrac{4,48}{22,4}=0,2mol\\ CO_2+Ca\left(OH\right)_2\rightarrow CaCO_3+H_2O\\ n_{CO_2}=n_{CaCO_3}=0,2mol\\ m_{CaCO_3}=0,2.100=20g\\ b/BTNT\left(O\right):2n_{CO_2}=n_{H_2O}\\ \Rightarrow n_{H_2O}=0,2.2=0,4mol\\ BTNT\left(H\right):2n_{H_2O}=n_{HCl}\\ n_{HCl}=0,4.2=0,8mol\\ V_{HCl}=\dfrac{0,8}{0,4}=2l\)
9 tháng 1 2017
Đáp án B
Gọi x là số mol CO2 (tương đương V lít).
Lúc cho V lít CO2 thu được x mol kết tủa CaCO3.
Cho cho V+3,36 lít CO2 vào thì chỉ thu được 2/3 lượng kết tủa tức 2x/3 mol CaCO3.
Vậy lượng 0,15 mol CO2 thêm vào đã tạo thêm một lượng kết tủa và hòa tan lượng kết tủa đó và hòa tan thêm x/3 mol kết tủa nữa
20 tháng 9 2023
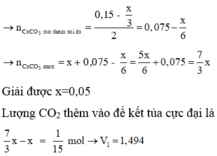
\(n_{Ca\left(OH\right)_2}=0,32\left(mol\right)\)
\(n_{KOH}=0,6\left(mol\right)\)
\(n_{CaCO_3}=\dfrac{10}{100}=0,1\left(mol\right)\)
PTHH :
\(CO_2+Ca\left(OH\right)_2\rightarrow CaCO_3\downarrow+H_2O\)
0,1 0,32 0,1
Ca(OH)2 dư nên tính theo CaCO3
\(CO_2+2KOH\rightarrow K_2CO_3+H_2O\)
0,3 0,6
\(V_{CO_2}=\left(0,1+0,3\right).22,4=8,96\left(l\right)\)
28 tháng 6 2021
a, Ta có : \(\left\{{}\begin{matrix}n_{CaCO3}=\dfrac{m}{M}=0,2\left(mol\right)\\n_{Ca\left(OH\right)2}=C_M.V=0,4\left(mol\right)\end{matrix}\right.\)
\(BTNT\left(Ca\right):n_{Ca\left(HCO_3\right)_2}=n_{Ca\left(OH\right)2}-n_{CaCO3}=0,2\left(mol\right)\)
\(BTNT\left(C\right):n_{CO2}=n_{CaCO3}+2n_{Ca\left(HCO3\right)2}=0,6\left(mol\right)\)
\(\Rightarrow V_{CO2}=13,44l\)
b, Ta có : \(\left\{{}\begin{matrix}n_{BaCO3}=\dfrac{m}{M}=0,025\left(mol\right)\\n_{Ba\left(OH\right)2}=C_M.V=0,2\left(mol\right)\end{matrix}\right.\)
\(BTNT\left(Ba\right):n_{Ba\left(HCO_3\right)_2}=n_{Ba\left(OH\right)2}-n_{BaCO3}=0,175\left(mol\right)\)
\(BTNT\left(C\right):n_{CO2}=n_{BaCO3}+2n_{Ba\left(HCO3\right)2}=0,375\left(mol\right)\)
\(\Rightarrow V_{CO2}=8,4l\)
c, Ta có : \(1< T=\dfrac{n_{NaOH}}{n_{SO2}}=1,875< 2\)
- Áp dụng phương pháp đường chéo :
Ta được : \(\dfrac{n_{NaHSO3}}{n_{Na2SO3}}=\dfrac{1}{7}\)
\(\Leftrightarrow7n_{NaHSO3}-n_{Na2SO3}=0\)
\(BTNT\left(Na\right):n_{NaHSO3}+2n_{Na2SO3}=0,375\)
\(\Rightarrow\left\{{}\begin{matrix}n_{NaHSO3}=0,025\\n_{Na2SO3}=0,175\end{matrix}\right.\)
\(\Rightarrow m_M=24,65g\)
19 tháng 4 2019
Đáp án B
Ta có: nCa(OH)2= 0,5.0,02= 0,01 mol;
nCaCO3= 0,5/100= 0,005 mol
Ta có: nCa(OH)2 > nCaCO3 và đề hỏi giá trị tối thiểu của V nên khi đó Ca(OH)2 dư
CO2 + Ca(OH)2 → CaCO3 ↓ + H2O
Theo PT: nCO2= nCaCO3= 0,005 mol
→ VCO2= 0,005.22,4= 0,112 lít