Cho tam giác ABC vuông tại A. Lấy điểm M trên AC (M khác A, C). Từ C vẽ đường thẳng vuông góc vs BM, đường thẳng này cắt BM ở D và cắt BA ở E.
1, CMR : \(\widehat{EAD}=\widehat{ECB}\).
2, CMR : EM \(\perp\)BC và tổng BM*BD + CM*CA ko đổi khi M di chuyển trên AC (khác A & C).
3, Kẻ DH \(\perp\) BC tại H. Gọi Q là trung điểm DH. Qua D kẻ đường thẳng DP \(\perp\) CQ (P \(\in\) BC). CM P là trung điểm BH.


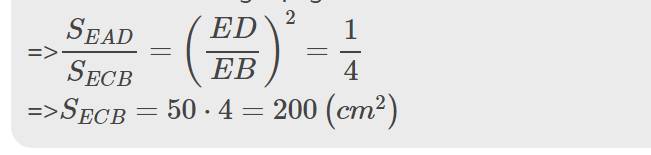
1: Xét ΔEAC vuông tạiA và ΔEDB vuông tại D có
góc E chung
Do đó: ΔEAC\(\sim\)ΔEDB
Suy ra: EA/ED=EC/EB
hay EA/EC=ED/EB
Xét ΔEAD và ΔECB có
EA/EC=ED/EB
góc AED chung
Do đó: ΔEAD\(\sim\)ΔECB
Suy ra: \(\widehat{EAD}=\widehat{ECB}\)
2: Xét ΔCEB có
CAlà đường cao
BD là đường cao
CA cắt BD tại M
Do đó: EM\(\perp\)BC