cmr phương trình :x5+x4+3x2-2x=1=0 có nghiệm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 11 2019
Đặt x 2 = t ≥ 0 ta được t 2 + 1 − 3 t + 2 4 − 2 3 = 0
Ta có: Δ = 1 − 3 2 − 4.2 4 − 2 3
= 4 − 2 3 − 8 4 − 2 3 = − 7 4 − 2 3 < 0
Suy ra phương trình ẩn t vô nghiệm hay phương trình đã cho cũng vô nghiệm.
Đáp án cần chọn là: D
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1 2024
a.
\(x^3-7x+6=0\)
\(\Leftrightarrow x^3-3x^2+2x+3x^2-9x+6=0\)
\(\Leftrightarrow x\left(x^2-3x+2\right)+3\left(x^2-3x+2\right)=0\)
\(\Leftrightarrow\left(x^2-3x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left(x^2-x-2x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[x\left(x-1\right)-2\left(x-1\right)\right]\left(x+3\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=2\\x=-3\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1 2024
f.
\(x^4-4x^3+12x-9=0\)
\(\Leftrightarrow x^4-4x^3+3x^2-3x^2+12x-9=0\)
\(\Leftrightarrow x^2\left(x^2-4x+3\right)-3\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow\left(x^2-4x+3\right)\left(x^2-3\right)=0\)
\(\Leftrightarrow\left(x^2-x-3x+3\right)\left(x^2-3\right)=0\)
\(\Leftrightarrow\left[x\left(x-1\right)-3\left(x-1\right)\right]\left(x^2-3\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)\left(x^2-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=3\\x=\pm\sqrt{3}\end{matrix}\right.\)
CM
18 tháng 12 2017
Chọn B.
Ta có:
x
4
-
3
x
2
+
m
=
0
Dựa vào đồ thị ta có phương trình có 3 nghiệm phân biệt khi -m-3 = -3 => m = 0
CM
18 tháng 12 2018
Chọn B.
Ta có:
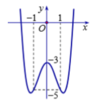
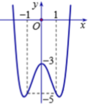
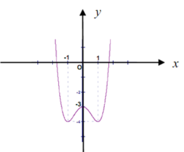
x 4 - 3 x 2 + m = 0 ⇔ x 4 - 3 x 2 = - m ⇔ x 4 - 3 x 2 - 3 = - m - 3 .
Dựa vào đồ thị ta có phương trình có 3 nghiệm phân biệt khi
- m - 3 = - 3 ⇔ m = 0 .
CM
16 tháng 5 2017
Đáp án C
x 4 − 3 x 2 + m = 0 ( 1 ) ⇔ x 4 − 3 x 2 − 3 = − 3 − m ( * )
Để phương trình (1) có 3 nghiệm phân biệt thì phương trình (*) có 3 nghiệm phân biệt
⇔ − 3 − m = − 3 ⇔ m = 0
CM
20 tháng 2 2017
Đáp án A
Xét hàm số f x = x 4 − 3 x 2 ,
có f ' x = 4 x 3 − 6 x = 0 ⇔ x = 0 x = ± 6 2 .
Tính các giá trị f 0 = 0 ; f ± 6 2 = − 9 4
=> Đồ thị (C) của hàm số y=f(x) .
Để phương trình f x = m + 1 có 2 nghiệm phân biệt
⇔ m + 1 > 0 m + 1 = − 9 4 ⇔ m > − 1 m = − 13 4
CM
8 tháng 4 2017
- x 4 + 3 x 2 + m = 0 ⇔ - x 4 + 3 x 2 + 1 = m + 1
Số nghiệm của phương trình là số giao điểm của đồ thị (C) với đường thẳng y = m + 1
Dựa vào đồ thị, phương trình có 3 nghiệm phân biệt m + 1 = 1 nên m = 0
Đáp án cần chọn là A
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 3 2020
1.
a/ \(\Leftrightarrow\left(x+1\right)\left(x^2+3x+2\right)+\left(x-1\right)\left(x^2-3x+2\right)-12=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2\right)+3x\left(x+1\right)-3x\left(x-1\right)+\left(x-1\right)\left(x^2+2\right)-12=0\)
\(\Leftrightarrow2x\left(x^2+2\right)+6x^2-12=0\)
\(\Leftrightarrow x^3+3x^2+2x-6=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+4x+6\right)=0\Rightarrow x=1\)
b/ Nhận thấy \(x=0\) ko phải nghiệm, chia 2 vế cho \(x^2\)
\(x^2+\frac{1}{x^2}+3\left(x+\frac{1}{x}\right)+4=0\)
Đặt \(x+\frac{1}{x}=t\Rightarrow x^2+\frac{1}{x^2}=t^2-2\)
\(t^2-2+3t+4=0\Rightarrow t^2+3t+2=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{1}{x}=-1\\x+\frac{1}{x}=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x^2+x+1=0\left(vn\right)\\x^2+2x+1=0\end{matrix}\right.\) \(\Rightarrow x=-1\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 3 2020
1c/
\(\Leftrightarrow x^5+x^4-2x^4-2x^3+5x^3+5x^2-2x^2-2x+x+1=0\)
\(\Leftrightarrow x^4\left(x+1\right)-2x^3\left(x+1\right)+5x^2\left(x+1\right)-2x\left(x+1\right)+x+1=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^4-2x^3+5x^2-2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^4-2x^3+5x^2-2x+1=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow x^4-2x^3+x^2+x^2-2x+1+3x^2=0\)
\(\Leftrightarrow\left(x^2-x\right)^2+\left(x-1\right)^2+3x^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-x=0\\x-1=0\\x=0\end{matrix}\right.\) \(\Rightarrow\) không tồn tại x thỏa mãn
Vậy pt có nghiệm duy nhất \(x=-1\)
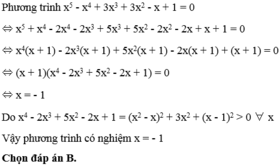
Ta có:
Đặt phương trình là f(x): x5 + x4 +3x2-2x-1.
f(1) = 2
f(-2) = -1
f(1) × f(-2) = -2 < 0
=> có 1 nghiệm trong khoảng từ (1; -2)
=>Pt có nghiệm (dpcm)