Cho tam giác ABC cân tại A (\(\widehat{A}=120^O\)).AI là tia phân giác của góc A (I \(\in\)BC). Từ I hạ IH\(\perp\)AB (H\(\in\)AB), IK\(\perp\)AC (K\(\in\)AC).
A) Chứng minh tam giác IKH đều và HK//BC.
B) Trên tia đối của tia AB lấy điểm D sao cho AD=AB.Chứng minh tam giác ACD đều.
C) Có nhận xét gì về tam giác BCD? Chứng...
Đọc tiếp
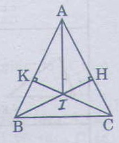
Cho tam giác ABC cân tại A (\(\widehat{A}=120^O\)).AI là tia phân giác của góc A (I \(\in\)BC). Từ I hạ IH\(\perp\)AB (H\(\in\)AB), IK\(\perp\)AC (K\(\in\)AC).
A) Chứng minh tam giác IKH đều và HK//BC.
B) Trên tia đối của tia AB lấy điểm D sao cho AD=AB.Chứng minh tam giác ACD đều.
C) Có nhận xét gì về tam giác BCD? Chứng minh.
a: Xét ΔAKI vuông tại K và ΔAHI vuông tại H có
AI chung
\(\widehat{KAI}=\widehat{HAI}\)
Do đó: ΔAKI=ΔAHI
Suy ra: IH=IK và AK=AH
Xét ΔIHK có IH=IK
nên ΔIKH cân tại I
mà \(\widehat{KIH}=60^0\)
nên ΔIKH đều
Xet ΔABC có AK/AC=AH/AB
nên KH//BC
b: Xét ΔACD có AC=AD
nên ΔACD cân tại A
mà \(\widehat{CAD}=60^0\)
nên ΔACD đều
c: Xét ΔBCD có
CA là đường trung tuyến
CA=BD/2
Do đo ΔCBD vuông tại C