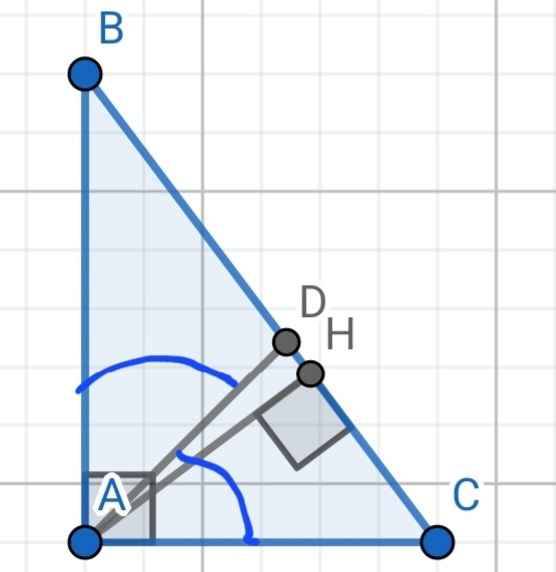
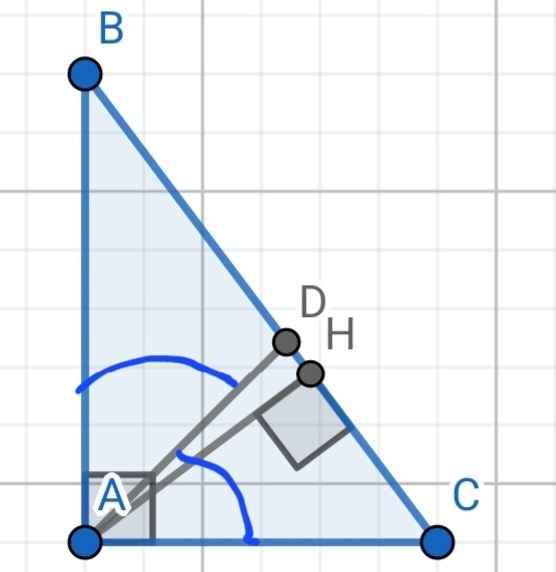
cho tam giác ABC vuông tại A, AB=8cm, AC=6cm,AD là tia phân giác góc A, D ∈BC
a) Tính \(\dfrac{DB}{DC}\)
b) Tính BC, từ đó tính DB,DC làm tròn kết quả 2 chữ số thập phân
c) Kẻ đường cao AH (H∈BC) . Chứng minh rằng: ΔAHB đồng dạng với ΔCHA . Tính \(\dfrac{S\Delta AHB}{S\Delta CHA}\)
d) tính AH


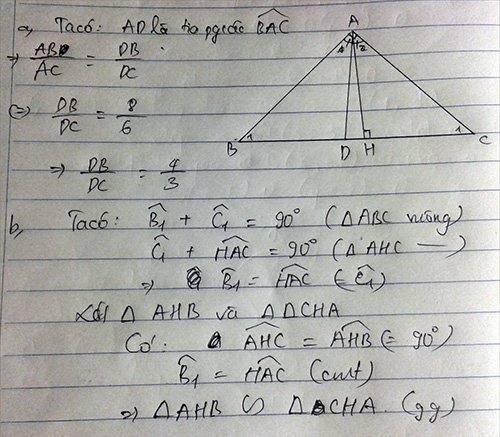
A B C 8 6 cm cm
Xét ΔABC có AD là phân giác của góc A
=>\(\dfrac{DC}{AC}=\dfrac{BD}{BA}\Rightarrow\dfrac{BD}{DC}=\dfrac{AB}{AC}=\dfrac{8}{6}=\dfrac{4}{3}\)
b) Xét ΔABC có góc A=90o theo đl py-ta-go ta đc
BC=10cm
a) Trong ΔABC có AD là phân giác ∠A
Áp dụng tính chất đường phân giác vào ΔABC, ta có:
\(\frac{AB}{AC}=\frac{DB}{DC}\)
hay \(\frac{8}{6}=\frac{4}{3}=\frac{DB}{DC}\)
b) Áp dụng định lí Py-ta-go vào ΔvuôngABC, ta có:
BD2 = AB2 + AC2
hay BD2 = 82 + 62 = 64 + 36 = 100
=> BD = 10(cm)
Áp dụng tính chất đường phân giác vào ΔABC, ta có:
\(\frac{AC}{AB}=\frac{DC}{DB}\)
=> \(\frac{AC}{AB+AC}=\frac{DC}{DC+DB}\)
hay \(\frac{6}{14}=\frac{DC}{10}\)
=> DC = \(\frac{10.6}{14}=4,28\)(cm)
DB = BC - DC = 10 - 4,28 = 5,72(cm)