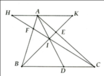
Cho điểm I nằm trong tam giác ABC. Các tia AI, BI, CI cắt các cạnh BC, AC, AB thứ tự ở D,E,F. Chứng minh: \(\dfrac{FA}{FB}+\dfrac{EA}{EC}=\dfrac{IA}{ID}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 1 2021
Từ A kẻ đường thẳng // BC cắt BO, CO kéo dài tại P và Q
Theo định lý Thales ta có: \(\frac{DB}{DC}=\frac{AP}{AQ},\frac{EC}{EA}=\frac{BC}{AP},\frac{FA}{FB}=\frac{AQ}{BC}\)
Nhân 3 đẳng thức vs nhau ta đc:
\(\frac{DB}{DC}.\frac{EC}{EA}.\frac{FA}{FB}=\frac{AP}{AQ}.\frac{BC}{AP}.\frac{AQ}{BC}=1\) ( ĐPCM)
CM
15 tháng 12 2018
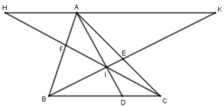
Qua A kẻ đường thẳng song song với BC, cắt CF, BE lần lượt tại H, K
AH // BC nên theo định lí Talet ta có: A F F B = A H B C
AK //BC nên theo định lí Talet ta có: A E E C = A K B C
Suy ra A F F B + A E E C = A H B C + A K B C = H K C B hay A F F B + A E E C = K H B C (1)
Lại có: AH // DC nên theo định lí Talet ta có: A I I D = A H D C
AK // BD nên theo định lí Talet ta có: A I I D = A K B D
Do đó A I I D = A H D C = A K B D (2)
Theo tính chất dãy tỉ số bằng nhau A H D C = A K B D = A I + A K D C + B D = H K B C (3)
Từ (2) và (3) suy ra A I I D = H K B C (4)
Từ (1) và (4) suy ra A F F B + A E E C = A I I D
Đáp án B
23 tháng 1 2022
áp dụng định lý phân giác ta có:\(\left\{{}\begin{matrix}\dfrac{DB}{DC}=\dfrac{AB}{AC}\\\dfrac{EC}{EA}=\dfrac{BC}{AB}\\\dfrac{FA}{FB}=\dfrac{AC}{BC}\end{matrix}\right.\)
\(\dfrac{DB}{DC}.\dfrac{EC}{EA}.\dfrac{FA}{FB}=\dfrac{AB}{AC}.\dfrac{BC}{AB}.\dfrac{AC}{BC}=1\)