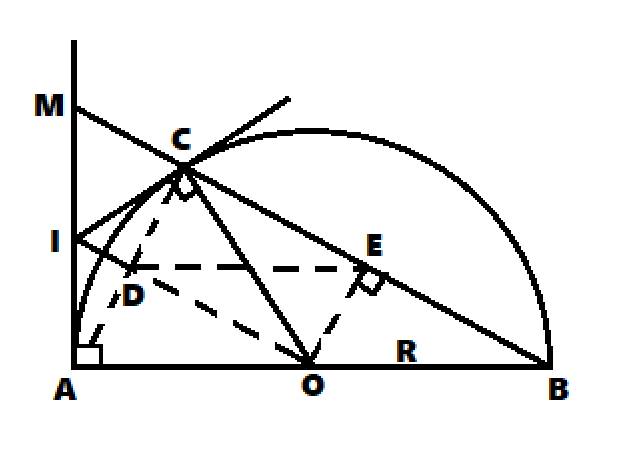
Cho nửa đường tròn (O) đường kính AB. Trên tia đối của tia AB lấy một điểm M. Vẽ tiếp tuyến MC với nửa đường tròn. Gọi H là hình chiếu của C trên AB
a, c/m tia CA là tia phân giác của góc MCH
b, Giả sử MA=a, MC=2a. Tinh AB và CH theo a