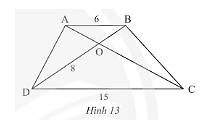
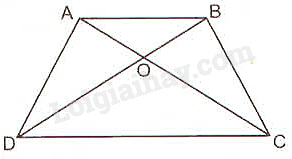
cho hình thang ABCD \(\left(AB//CD\right)\)có AB<CD. gọi O là giao điểm 2 đường chéo, S là giao điểm của 2 đường thẳng chứa 2 cạnh bên.Đường thẳng SO cắt AB, CD theo thứ tự tại M,N.CMR
a,\(\dfrac{MA}{ND}=\dfrac{MB}{NC};\dfrac{MA}{NC}=\dfrac{MB}{ND}\)
b,\(MA=MB;NC=ND\)