Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
Suy ra: BD=CE
b: Xét ΔAED có AE=AD
nên ΔAED cân tại A
c: Xét ΔEBI vuông tại E và ΔDCI vuông tại D có
EB=DC
\(\widehat{EBI}=\widehat{DCI}\)
Do đó; ΔEBI=ΔDCI
Suy ra: IB=IC
Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc BAC
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó:ΔABD=ΔACE
b: Xét ΔADI vuông tại D và ΔAEI vuông tại E có
AI chung
AD=AE
Do đó: ΔADI=ΔAEI
Suy ra: \(\widehat{DAI}=\widehat{EAI}\)
hay AI là tia phân giác của góc BAC
c: Xét ΔADE có AD=AE
nên ΔADE cân tại A
a: Xét ΔBEC vuông tại E và ΔCDB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔBEC=ΔCDB
b: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó:ΔABD=ΔACE
Suy ra: AD=AE
c: Ta có: ΔBEC=ΔCDB
nên \(\widehat{IBC}=\widehat{ICB}\)
hayΔIBC cân tại I
Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó:ΔABI=ΔACI
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc BAC
d: Xét ΔABC có AE/AB=AD/AC
nên DE//BC
a) Xét ΔAEC vuông tại E và ΔADB vuông tại D có
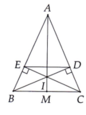
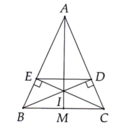
AC=AB(ΔABC cân tại A)
\(\widehat{BAD}\) chung
Do đó: ΔAEC=ΔADB(cạnh huyền-góc nhọn)
Suy ra: AE=AD(hai cạnh tương ứng)
Xét ΔAED có AE=AD(cmt)
nên ΔAED cân tại A(Định nghĩa tam giác cân)
Xét tam giác vuông AEC và tam giác vuông ADB,có:
Góc A: chung
AB=AC ( ABC cân )
Vậy tam giác vuông AEC và tam giác vuông ADB ( ch.gn )
=> BD=CE ( 2 cạnh tương ứng )
b. bạn xem lại đề nhé
). Kẻ BD vuông góc AC, CE vuông góc AB (D thuộc cạnh AC, E thuộc cạnh AB).
a) xét 2 tam giác , ta có :
\(\stackrel\frown{E}\) = \(\stackrel\frown{D}\)= 90
=> tam giác vuông
\(\stackrel\frown{A}\) chung
AB=AC
=> 2 tam giác bằng nhau(g-c-g)
b, xét 2 tam giác ABH và ACH
AB=AC
AH chung
góc B = góc C
=> 2 tam giác bằng nhau
=> đpcm
c) Áp dụng định nghĩa của trọng tâm tam giác => AH > HC