tìm tham số a,b để:
đa thức P(x) = ax3 + (a + 1)x2 - (4b + 3)x - 5b đồng thời chia hết cho (x -1) và ( x + 2)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Để hai đa thức trên chia cho nhau hết thì :\(\left\{{}\begin{matrix}7a-4=0\\b-2\left(1-3a\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7a=4\\6a+b=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{4}{7}\\b=-\dfrac{10}{7}\end{matrix}\right.\)
Vậy ...

b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)

+ P(x) chia hết cho x + 1
⇔ P(-1) = 0
⇔ m . ( - 1 ) 3 + ( m – 2 ) ( - 1 ) 2 – ( 3 n – 5 ) . ( - 1 ) – 4 n = 0
⇔ -m + m – 2 + 3n – 5 – 4n = 0
⇔ -n – 7 = 0
⇔ n = -7 (1)
+ P(x) chia hết cho x – 3
⇔ P(3) = 0
⇔ m.33 + (m – 2).32 – (3n – 5).3 – 4n = 0
⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0
⇔ 36m – 13n = 3 (2)
Từ (1) và (2) ta có hệ phương trình :
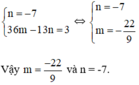

+ P(x) chia hết cho x + 1
⇔ P(-1) = 0
⇔ m.(-1)3 + (m – 2)(-1)2 – (3n – 5).(-1) – 4n = 0
⇔ -m + m – 2 + 3n – 5 – 4n = 0
⇔ -n – 7 = 0
⇔ n = -7 (1)
+ P(x) chia hết cho x – 3
⇔ P(3) = 0
⇔ m.33 + (m – 2).32 – (3n – 5).3 – 4n = 0
⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0
⇔ 36m – 13n = 3 (2)
Từ (1) và (2) ta có hệ phương trình :
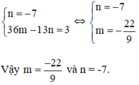

\(\dfrac{H\left(x\right)}{x-1}=\dfrac{ax^3+ax^2+x^2-4bx-3x+5b}{x-1}\)
\(=\dfrac{ax^3-ax^2+x^2\cdot\left(2a+1\right)-2ax-x+\left(2a-4b-2\right)x-2a+4b+2+b-2+2a}{x-1}\)
\(=ax^2+x\left(2a+1\right)+\left(2a-4b-2\right)+\dfrac{b+2a-2}{x-1}\)
\(\dfrac{H\left(x\right)}{x+2}\)
\(=\dfrac{ax^3+\left(a+1\right)x^2-\left(4b+3\right)x+5b}{x+2}\)
\(=\dfrac{ax^3+2ax^2+x^2\left(-a+1\right)+x\cdot\left(-2a+2\right)+[-x\left(-2a+2\right)-\left(4b+3\right)x]+5b}{x+2}\)
\(=ax^2+\left(-a+1\right)\cdot x+\dfrac{\left[2ax-2x-4bx-3x\right]+5b}{x+2}\)
\(=ax^2-ax+x+\dfrac{-5x+2ax-4bx-10+4a-8b+10-4a+13b}{x+2}\)
\(=ax^2-ax+x+\left(2a-4b-5\right)+\dfrac{-4a+13b+10}{x+2}\)
Theo đề, ta có hệ:
-4a+13b=-10 và b+2a=2
=>a=6/5; b=-2/5

a: \(\Leftrightarrow2x^4-2x^3+2x^2+3x^3-3x^2+3x-2x^2+2x+2+a-2⋮x^2-x+1\)
=>a=2

A(x)=(1-x^n)(1+x^n)/(1-x)(1+x)
B(x)=1-x^n/1-x
A(x) chia hết cho B(x) khi 1-x^n chia hết cho 1+x
x^n+1/x+1=A(x)+(1+(-1)^n)/(x+1)
=>1-x^n chia hết cho 1+x khi và chỉ khi n=2k+1
Lời giải:
Áp dụng định lý Bezout về số dư đa thức thì số dư của $P(x)$ khi chia cho $x-1$ và $x+2$ lần lượt là $P(1)$ và $P(-2)$
Có:
\(P(1)=a+a+1-(4b+3)-5b\)
\(P(-2)=-8a+4(a+1)+2(4b+3)-5b\)
Để \(P(x)\vdots x-1; P(x)\vdots x+2\Rightarrow P(1)=P(-2)=0\)
\(\Leftrightarrow \left\{\begin{matrix} 2a-9b-2=0\\ -4a+3b+10=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} 2a-9b=2\\ -4a+3b=-10\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=\frac{14}{5}\\ b=\frac{2}{5}\end{matrix}\right.\)