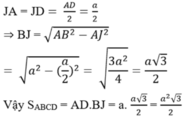Cho hình bình hành ABCD, trên tia đối của tia BA lấy điểm E, trên tia đối củatia DA lấy điểm K. Đường thẳng ED cắt KB tại O. Chứng minh rằng diện tích tứ giácABOD và CEOK bằng nhau
Akai Haruma, nhờ cô giúp giùm!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác BDCE có
BE//CD
BE=CD
Do đó: BDCE là hình bình hành

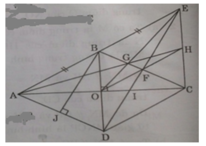
b) Xét Δ BCD có: O là trung điểm của BD
F là trung điểm của BC
⇒ OF là đường trung bình của ΔBDC ⇒ OF // DC mà DC // AB nên OF // AE
⇒ FH // BE
Mà O là trung điểm của AC nên H là trung điểm của EC hay AH là trung tuyến của ΔAEC. Mà AH cắt EO tại G nên G là trong tâm của ΔAEC ⇒ A, G, H thẳng hàng.

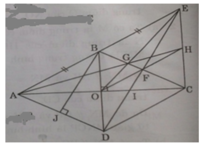
a) Ta có BE = BA (gt) mà BA // CD và BA = CD (gt)
⇒ BE // CD và BE = CD.
Do đó BECD là hình bình hành nên F là trung điểm của BC.
Xét ΔBDC có I là trọng tâm ⇒ ID = 2IF.

c) ΔABD cân (AB = AD (gt)) có ∠BAD = 60o nên ΔABD đều
kẻ BJ ⊥ AD ta có: