Cho hình bình hành ABCD có diện tích=24 cm vuông, O là giao điểm của 2 đường chéo. Khoảng cách từ O đến AD,CD lần lượt =2;3 cm. Tính độ dài AD,CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
13 tháng 2 2022
tk hen:
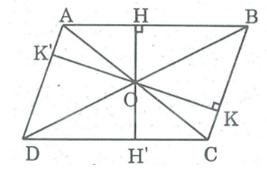
Gọi O là giao điểm hai đường chéo của hình bình hành ABCD, khoảng cách từ O đến cạnh AB là OH = 2cm , đến cạnh BC là OK = 3cm
* Kéo dài OH cắt cạnh CD tại H'.
Ta có OH ⊥ BC
⇒ OH' ⊥ CD và OH' = 2cm
Suy ra HH' bằng đường cao của hình bình hành.
= HH'.AB ⇒ 
* Kéo dài OK cắt AD tại K'.
Ta có: OK ⊥ BC ⇒ OK' ⊥ CD và OK' = 3 (cm)
Suy ra KK' là đường cao của hình bình hành.
= KK'.AB ⇒ 
Chu vi của hình bình hành ABCD là (6 + 4).2 = 20 (cm).
14 tháng 1 2022
a: Xét ΔMOB vuông tại O và ΔNOD vuông tại O có
OB=OD
\(\widehat{MBO}=\widehat{NDO}\)
Do đó: ΔMOB=ΔNOD
Suy ra: OM=ON
c: Xét tứ giác MBND có
O là trung điểm của MN
O là trung điểm của BD
Do đó: MBND là hình bình hành
mà MN\(\perp\)BD
nên MBND là hình thoi
LL
13 tháng 6 2019
a,Hình bình hành ABCD có AB=CD
⇒12AB=AM=12CD=CN⇒12AB=AM=12CD=CN
Mặt khác, M,N lần lượt là trung điểm của AB và CD
Do đó, AM//CN
Tứ giác AMCN có cặp cạnh đối vừa song song vừa bằng nhau nên là hình bình hành (đpcm)
b, Tứ giác AMCN là hình bình hành
⇒⇒M1ˆ=N1ˆM1^=N1^ (Hai góc đối của hình bình hành AMCN)
⇒⇒M2ˆ=N2ˆM2^=N2^ (Do M1ˆM1^ và M2ˆM2^ là hai góc kề bù; N1ˆN1^ và N2ˆN2^ là hai góc kề bù)
Mặt khác, ABCD là hình bình hành nên AB//CD ⇒⇒B1ˆ=D1ˆB1^=D1^
ΔEDNΔEDN và ΔKBMΔKBM có:
M2ˆ=N2ˆM2^=N2^
DN=BMDN=BM
B1ˆ=D1ˆB1^=D1^
⇒ΔEDN=ΔKBM(g.c.g)⇒ΔEDN=ΔKBM(g.c.g)
⇒ED=KB⇒ED=KB (đpcm)
c, Gọi O là giao điểm của AC và BD.
ABCD là hình bình hành
⇒OA=OC⇒OA=OC
ΔCABΔCAB có:
MA=MBMA=MB
OA=OCOA=OC
MC cắt OB tại K
⇒⇒ K là trọng tâm của ΔCABΔCAB
Mặt khác, I là trung điểm của BC
⇒⇒ IA,OB,MC đồng quy tại K
Hay AK đi qua trung điểm I của BC (đpcm)