E đang học lý phần quang học 1. Có nhiều bài liên quan đến đạo hàm, nguyên hàm, tích phân và vi phân. Cho e hỏi đạo hàm, tích phân, nguyên hàm, vi phân, log, ln, lim thực ra là gì ạ. Cách tính nhanh các giá trị trên là gì. Và làm sao để biết khi nào dùng đạo hàm, khi nào dùng nguyên hàm, khi nào dùng tích phân, vi phân ạ. E đang cần gấp. Làm ơn giúp e
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Ta có ∫ 0 1 f ' x . c o s π x d x
= ∫ 0 1 c o s π x d f x = f x . c o s π x 0 1 − ∫ 0 1 f x . c o s π x ' d x
= − f 1 + f 0 + π ∫ 0 1 f x . sin π x d x = π 2 ⇒ ∫ 0 1 f x . sin π x d x = 1 2 .
Xét ∫ 0 1 f x + k . sin π x 2 d x = 0
⇔ ∫ 0 1 f 2 x d x + 2 k . ∫ 0 1 f x . sin π x d x + k 2 . ∫ 0 1 sin 2 π x d x = 0
⇔ 1 2 k 2 + 2 k . 1 2 + 1 2 = 0 ⇔ k + 1 2 = 0 ⇔ k = − 1.
Suy ra ∫ 0 1 f x − sin π x 2 d x = 0.
Vậy f x = sin π x ⇒ ∫ 0 1 f x d x = ∫ 0 1 sin π x d x = 2 π .

Đáp án A
Đặt t = x ⇔ d t = d x 2 x ⇔ d x = 2 d t ; x = 0 ⇒ t = 0 x = 4 ⇒ t = 2
Khi đó I = ∫ 0 4 f ' x d x = ∫ 0 2 2 t . f ' t d t = 2 ∫ 0 2 t . f ' t d t
Đặt u = t d v = f ' t d t ⇔ d u = d t v = f t ⇒ 2 ∫ 0 2 t . f ' t d t = t . f t 0 2 - ∫ 0 2 f t d t = 2 f 2 - 1 = - 5
Vậy tích phân I = 2 . - 5 = - 10 .

Đáp án C.
Ta có I = ∫ 0 2 f x g x ' d x = ∫ 0 2 f ' x g x + g ' x f x d x
= ∫ 2 g x f ' x d x + ∫ 2 g ' x f x d x = 5.
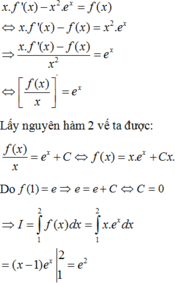
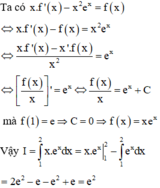
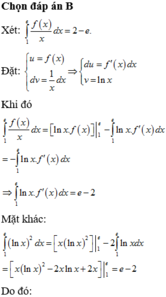
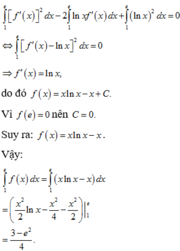
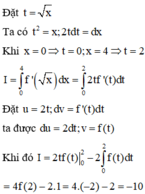
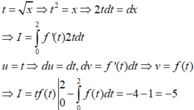
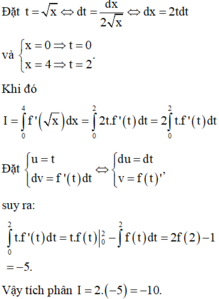
Đây là một câu hỏi rất rộng. Để biết khi nào dùng đạo hàm, nguyên hàm, ... thì bạn cần phải học về khái niệm của các đại lượng trên, cách tính và ý nghĩa của nó như thế nào.
Ví dụ về đạo hàm chẳng hạn.
Người ta định nghĩa đạo hàm thế này:
Hàm số \(y=f(x)\) xác định trên tập \(D\)
Tại giá trị \(x=x_0\) thì \(y=y_0\)
Tại giá trị \(x=x_1\) thì \(y=y_1\)
Ta có biến thiên của hàm số là: \(\Delta y=y_1-y_0\)
Biến thiên của đối số là: \(\Delta x = x_1-x_0\)
Ta gọi giới hạn nếu có của tỉ số \(\dfrac{\Delta y}{\Delta x}\) khi \(\Delta x\) tiến đến 0 là đạo hàm bậc nhất của hàm số \(y=f(x)\) tại \(x=x_0\)
Viết là: \(y'=\lim\limits_{\Delta x\rightarrow0}\dfrac{\Delta y}{\Delta x}\)
Ý nghĩa của đạo hàm
Trong chuyển động thẳng không đều, khi gắn chuyển động vào một hệ quy chiếu (có hệ tọa độ và mốc thời gian), thì để xác định vận tốc của chuyển động ta tìm:
+ Vận tốc trung bình: \(v_{TB}=\dfrac{\Delta x}{\Delta t}\)
+ Để xác định vận tốc tức thời tại một vị trí, ví dụ tại M ở hình vẽ trên thì ta phải cho N tiến sát đến M, hay \(\Delta t \rightarrow 0\)
Từ đó suy ra: \(v=\lim\limits_{\Delta t\rightarrow0}\dfrac{\Delta x}{\Delta t}\), theo khái niệm đạo hàm ta có giá trị này bằng đạo hàm bậc nhất của tọa độ \(x\) theo thời gian \(t\), viết lại là:
\(v=x'_{(t)}\)
Tương tự ta có gia tốc của chuyển động: \(a=v'_{(t)}\)
Ví dụ: Xét một chuyển động thẳng biến đổi đều có phương trình là:
\(x=10+3.t+2t^2\) (m)
Suy ra phương trình vận tốc là: \(v=x'_{(t)}=3+6.t (m/s)\)
Gia tốc của chuyển động là: \(a=v'_{(t)}=6(m/s^2)\)
Vậy nhé, còn các đại lượng khác thì bạn tìm hiểu trong sách Giải tích 12 sẽ rõ.
E xin Cảm ơn ạ.