Một đội sản xuất làm 1000 sản phẩm trong một thời gian quy định.Nhờ tăng năng suất lao động mỗi ngày đội làm thêm được 10 sản phẩm so với kế hoạch.Vì vậy không những đã làm vượt kế hoạch 80 sản phẩm mà còn hoàn thành công việc trước 2 ngày so với quy định.Tính số sản phẩm mà đội phải làm trong 1 ngày theo kế hoạch.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

| KLCV | Năng suất | Thời gian | |
| Kế hoạch | 1000 | x | \(\dfrac{1000}{x}\) |
| Thực tế | 1000+80=1080 | x+10 | \(\dfrac{1080}{x+10}\) |
Pt: \(\dfrac{1000}{x}-\dfrac{1080}{x+10}=2\)
Gọi số sản phẩm đội dự định làm mỗi ngày là x \(\left(x\in N,x< 100\right)\)( sản phẩm )
Theo kế hoạch
Thời gian hoàn thành là:\(\dfrac{1000}{x}\left(ngày\right)\)
Thực tế.
Mỗi ngày tổ làm được x+10 ( sản phẩm).
Thời gian hoàn thành : \(\dfrac{1080}{x+10}\)( ngày)
Vì thời gian thực tế ít hơn thời gian dự định là 2 ngày nên ta có phương trình:
\(\dfrac{1000}{x}-\dfrac{1080}{x+10}=2\)
\(\Leftrightarrow\dfrac{500}{x}-\dfrac{540}{x+10}=1\) ( quy đồng đơn giản hơn để dễ làm )
\(\Leftrightarrow\dfrac{500.\left(x+10\right)-540x}{x\left(x+10\right)}=\dfrac{x\left(x+10\right)}{x\left(x+10\right)}\)
\(\Leftrightarrow500x+5000-540x=x^2+10x\) (quy đồng bỏ mẫu )
\(\Leftrightarrow x^2+50x-5000=0\)
\(\Leftrightarrow\) pt có 2 nghiệm phân biệt
th1 : x=-100 ( vô lí)
th2 x= 50 ( nhận )
Vậy...
Gọi \(x\) (ngày) là số ngày hoàn thành theo kế hoạch (\(x\) > 2)
Số sản phẩm mỗi ngày theo kế hoạch: \(\dfrac{1000}{x}\) (sản phẩm)
Số sản phẩm mỗi ngày thực làm: \(\dfrac{1000}{x}+10\)
Số ngày thực làm: \(x-2\) (ngày)
Theo đề bài ta có phương trình:
\(\left(\dfrac{1000}{x}+10\right).\left(x-2\right)=1080\)
\(\Leftrightarrow1000-\dfrac{2000}{x}+10x-20=1080\)
\(\Leftrightarrow10x^2+980x-1080x-2000=0\)
\(\Leftrightarrow10x^2-100x-2000=0\)
\(\Leftrightarrow x^2-10x-200=0\)
\(\Leftrightarrow x^2-20x+10x-200=0\)
\(\Leftrightarrow\left(x^2-20x\right)+\left(10x-200\right)=0\)
\(\Leftrightarrow x\left(x-20\right)+10\left(x-20\right)=0\)
\(\Leftrightarrow\left(x-20\right)\left(x+10\right)=0\)
\(\Leftrightarrow x-20=0;x+10=0\)
*) \(x-20=0\)
\(\Leftrightarrow x=20\) (nhận)
*) \(x+10=0\)
\(x=-10\) (loại)
Vậy số sản phẩm theo kế hoạch đội đó phải làm trong một ngày là: \(\dfrac{1000}{20}=50\) (sản phẩm)

Gọi số sản phẩm đội dự định làm mỗi ngày là x (x ∈ ℕ * , x < 84) (sản phẩm)
*) Theo kế hoạch, thời gian hoàn thành là 1000/x (ngày)
*) Thực tế, mỗi ngày làm được x + 10 (sản phẩm)
Thời gian hoàn thành 1000/(x+10) (ngày)
Vì thời gian thực tế ít hơn thời gian dự định là 2 ngày nên ta có phương trình:
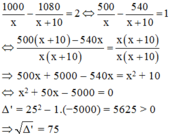
Phương trình có hai nghiệm phân biệt: x 1 = − 25 – 75 = −100 (loại)
và x 2 = −25 + 75 = 50 (tmđk)
Vậy theo kế hoạch, mỗi ngày tổ dự định làm 50 sản phẩm
Đáp án: C

Lời giải:
Giả sử năng suất ban đầu là $a$ sản phẩm/ ngày.
Số ngày dự định: $\frac{300}{a}$ (ngày)
Năng suất sau khi tăng: $a+5$ (sản phẩm/ ngày)
Số ngày hoàn thành sản phẩm: $\frac{300}{a+5}$ (ngày)
Theo bài ra: $\frac{300}{a}-\frac{300}{a+5}=3$
Giải pt trên, với điều kiện $a>0$ suy ra $a=20$
Vậy theo kế hoạch thì người thợ đó làm 20sp/ ngày
Gọi số sản phẩm phải làm trong 1 ngày là x
Theo đề, ta có: \(\dfrac{300}{x}-\dfrac{300}{x+5}=3\)
=>100/x-100/x+5=1
=>(100x+500-100x)/(x^2+5x)=1
=>x^2+5x-500=0
=>(x+25)(x-20)=0
=>x=20

Gọi số sản phầm dự định làm của tổ 1 là x, tổ 2 là y (x;y > 0)
Tổ 1 làm được \(115\%x=1,15x\) sản phầm
Tổ 2 làm được \(118\%x=1,18x\) sản phẩm
Ta có hpt:
\(\left\{{}\begin{matrix}x+y=810\\1,15x+1,18y=945\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=360\\y=450\end{matrix}\right.\)
Vậy, tổ 1 dự định làm 360 sản phẩm, tổ 2 dự định làm 450 sản phẩm.

Gọi số sản phẩm tổ 1 làm là x
Số sản phẩm tổ 2 làm là 1000-x
Theo đề, ta có: \(\dfrac{11}{10}x+\dfrac{6}{5}\left(1000-x\right)=1140\)
=>x=600
Vậy: Tổ 1 cần làm 600 sản phẩm
Tổ 2 cần làm 400 sản phẩm

Lời giải:
Gọi số sản phẩm tổ 1, 2 làm theo kế hoạch là $a,b$ (sản phẩm)
Tổng số sản phẩm phải làm: $a+b=900(1)$
Tổng số sản phẩm thực tế: $1,2a+1,3b=1130(2)$
Từ $(1); (2)\Rightarrow a=400; b=500$
Gọi số sản phẩm mà đội phải làm trong một ngày theo kế hoạch là x (\(x\in N\cdot\), x < 1000).
Khi đó thực tế mỗi ngày đội đó đã làm được là: x +10 (sản phẩm)
Thời gian đội phải làm theo kế hoạch là: \(\dfrac{1000}{x}\)(ngày)
Thời gian thực tế đội đã làm là: \(\dfrac{1080}{x+10}\)(ngày)
Theo đề bài ta có pt: \(\dfrac{1000}{x}\)-\(\dfrac{1080}{x+10}\) = 2
Đưa được về phương trình: x2 + 50x – 5000 = 0
Giải pt tìm được \(x_1=50,x_2=-100\) (loại)
Vậy theo kế hoạch mỗi ngày đội phải làm là 50 sản phẩm