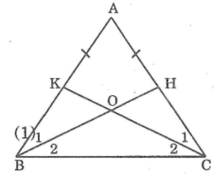
Cho tam giác ABC cân tại A lấy điểm H thuộc AC, đ iểm K thuộc AB. Sao cho AH=AK, Gọi O là giao điểm của BH và CK.Chứng minh: tam giác OBC là tam giác cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 1 2022
Xét ΔHBC và ΔKCB có
HC=KB
\(\widehat{HCB}=\widehat{KBC}\)
BC chung
Do đó: ΔHBC=ΔKCB
Suy ra: \(\widehat{HBC}=\widehat{KCB}\)
=>\(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O
PT
31 tháng 5 2017
Hình vẽ:
Giải:
Xét \(\Delta ABH\) và \(\Delta ACK\) có:
\(AH=AK\left(gt\right)\)
\(\widehat{A}\) là góc chung
\(AB=AC\) ( Vì \(\Delta ABC\) cân tại \(A\) )
Do đó: \(\Delta ABH=\Delta ACK\left(c.g.c\right)\)
\(\Rightarrow\widehat{B_2}=\widehat{C_2}\) ( cặp góc tương ứng )
Mà \(\widehat{B}=\widehat{C}\) ( Do \(\Delta ABC\) cân tại \(A\) )
\(\Rightarrow\widehat{B}-\widehat{B_2}=\widehat{C}-\widehat{C_2}\)
\(\Rightarrow\widehat{B_1}=\widehat{C_1}\)
\(\Rightarrow\Delta OBC\) cân tại \(O\) . \(\left(đpcm\right)\)
3 tháng 9 2016
Ta có : AK = AH ; AB = AC ; góc BAC chung
=> Tam giác ABH = tam giác ACK (c.g.c)
=> góc ABH = góc ACK mà góc ABC = góc ACB
=> Góc HBC = góc KCB => góc OBC = góc OCB => Tam giác OBC cân tại O
3 tháng 9 2016
Xét ΔAHB và ΔAKC có:
AB=AC(gt)
\(\widehat{A}\) : góc chung
AH=AK(gt)
=>ΔAHB=ΔAKC(c.g.c)
=>\(\widehat{ABH}=\widehat{ACK}\)
Có: \(\widehat{B}=\widehat{ABH}+\widehat{CBH}\)
\(\widehat{C}=\widehat{ACK}+\widehat{BCK}\)
Mà \(\widehat{B}=\widehat{C}\left(gt\right);\widehat{ABH}=\widehat{ACK}\left(cmt\right)\)
=> \(\widehat{CBH}=\widehat{BCK}\)
=>ΔOBC cân taaij O
3 tháng 9 2016
Bn vẽ hình đi nha
Giải
Cách 1
Do tam giác ABC cân tại A nên góc ABC=góc ACB và AB=AC
Do AB=AC mà AK=AH=> KB=HC
Xét tam giác BKC và tam giác CHB có:
-BK=HC
-góc ABC=góc ACB
-BC chung
=> tam giác BHC=tam giác CKB(c.g.c)
=>góc CHB=góc BKC
Xét tam giác KOB và tam giác HOC
-góc BKO=góc CHO
-BK=HK
-góc KOB=góc HOC
=>.tam giác KOB=tam giác HOC (g.c.g)
=>BO=CO ( chôc này bn có thể nói góc bằng nhau rồi cộng góc lại cx đc)
=> tam giác BOC cân tại O ( đpcm)
Cách 2
Xét tam giác ABH và tam giác ACK có
-AK=AH
-góc A chung
-AB=AC( tam giác ABC cân tại A)
=>góc ABH=góc ACB
=>góc HBC=góc KCB
=> tam giác OBC cân tại O ( Đpcm)
DL
14 tháng 1 2019
a) Xét tam giác BKC và tam giác CHB
+ BC chung
+ BK = HC vì AB = AC ; AK = AH => AB-AK=AC-AH
+ góc ABC = góc HCB (tam giác ABC cân)
Vậy tam giác BKC = tam giác CHB (c.g.c)
Và góc BKC = góc CHB
\(\widehat{KOB}=\widehat{HOC}\)(đối đỉnh)
\(\widehat{BKO}=\widehat{CHO}\left(cmt\right)\)
\(\Rightarrow\widehat{KBO}=\widehat{HCO}\)(3 góc trong tam giác)
Xét \(\Delta OKB\)và \(\Delta OHC\)
+ BK = HC
+ \(\widehat{KBO}=\widehat{OCH}\)
+ \(\widehat{OKB}=\widehat{OHC}\)
Vậy \(\Delta OKB=\Delta OHC\left(g.c.g\right)\)
VÀ OH = OK (hai cạnh tương ứng ) => Tam giác OKH cân tại O
OB = OC (hai cạnh tương ứng) => Tam giác OBC cân tại O
c) Xét \(\Delta AKO\)và \(\Delta AHO\)
+ AO chung
+ OK = OH
+ AH = AK
\(\Rightarrow\Delta AKO=\Delta AHO\left(c.c.c\right)\)
=> Góc KAO = góc HAO
Gọi giao điểm của KH và AO là F
Xét tam giác AFK và tam giác AFH
+ AK = AH
+ ÀF chung
+góc KAF = góc HAF (cmt)
Vậy tam giác AFK = tam giác AFH (c.g.c)
Và KF = FH(hai cạnh tương ứng)
Hay AO đi qua trung điểm của HK
CM
7 tháng 1 2018
+) Xét ΔABH và ΔACK, ta có:
AB = AC ( vì tam giác ABC cân tại A)
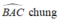
AH = AK (giả thiết)
Suy ra: ΔABH = ΔACK(c.g.c)
+ Do đó, tam giác OBC cân tại O.
Xét tam giác ABH và ACK có:
AH=AK(gt)
AB=AC(tam giác ABC cân)
Â:góc chung
=> ABH=ACK
=> Góc ABH= Góc ACK
=> Góc OBC= Góc OCB
=> OBC cân tại O
Ta có tam giác ABC là tam giác cân tại A AB=AC; B=C (tính chất tam giác cân) Xét tam giác ACK và tam giác ABH có: AK=AH(giả thiết) A chung AC=AB(giả thiết) => tam giác ACK=tam giác ABH(c.g.c) OBC=OCB(2 góc tương ứng) Ta có B=OBC + KBO C=OCB + HCO Mà B=C(giả thiết) KBO= HCO(cmt) => OBC= OCB => OBC là tam giác cân