Ở mặt nước, tại hai điểm A và B có hai nguồn kết hợp dao động cùng pha theo phương thẳng đứng. ABCD là hình vuông nằm ngang. Biết trên CD có 4 vị trí mà ở đó các phần tử dao động với biên độ cực tiểu. Trên AB có tối đa bao nhiêu vị trí mà phần tử ở đó dao động với biên độ cực đại?
A. 13
B. 7
C. 9
D. 11
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Trên AB có 15 vị trí dao động với biên độ cực đại do vậy ta có AB < 8λ
Xét M thuộc trên CD ta có
![]()
Vậy ![]()
Mặt khác M là cực đại giao thoa thì:
![]()
Do đó ta được
![]()
Vậy có 7 giá trị k; tương ứng có tối đa 7 cực đại giao thoa trên CD.

- Số cực đại trên CD thõa mãn điều kiện:
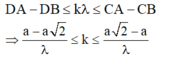
- Vì trên CD có 3 cực đại và các cực đại đối xứng qua cực đại k = 0 nên: -2 < k < 2
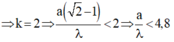
- Số cực đại trên AB:
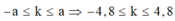
⇒ Số cực đại là 9.

Đáp án D
Số cực đại trên CD thõa mãn điều kiện :

Vì trên CD có 3 cực đại và các cực đại đối xứng qua cực đại k = 0 nên : -2 < k < 2

Số cực đại trên AB
![]()
Số cực đại là 9.

Đáp án D
Số cực đại trên CD thõa mãn điều kiện : D A - D B ≤ k λ ≤ C A - C B
⇒ a - a 2 λ ≤ k ≤ a 2 - a λ
Vì trên CD có 3 cực đại và các cực đại đối xứng qua cực đại k = 0 nên : -2 < k < 2
⇒ k = 2 ⇒ a ( 2 - 1 ) λ < 2 ⇒ a λ < 4 , 8
Số cực đại trên AB - a ≤ k ≤ a ⇒ - 4 , 8 ≤ k ≤ 4 , 8
Số cực đại là 9.

Đáp án B
Trên AB có 15 vị trí dao động với biên độ cực đại do vậy ta có A B < 8 λ
Xét M thuộc trên CD ta có d 2 − d 1 ≤ AB 2 − 1
Vậy d 2 − d 1 < 8 λ 2 − 1
Mặt khác M là cực đại giao thoa thì: d 2 − d 1 = kλ , với k = 0 , ± 1 , ± 2...
Do đó ta được kλ < 8 λ 2 − 1 ⇒ k < 3 , 3
Vậy có 7 giá trị k; tương ứng có tối đa 7 cực đại giao thoa trên CD



