biết phương trình 3x.2x2=1 tìm hai nghiệm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 6 2020
a, \(x^2-3x-6+4=0\)
\(\Leftrightarrow x^2-3x-2=0\)
Ta có : \(\left(-3\right)^2-4.\left(-2\right)=9+8=17>0\)
Nên có 2 nghiệm phân biệt
\(x_1=\frac{3-\sqrt{17}}{2};x_2=\frac{3+\sqrt{17}}{2}\)
b, Để PT có nghiệm thì \(\Delta=0\)
\(\Leftrightarrow b^2-4ac=0\)
\(\Leftrightarrow\left(-3\right)^2-4\left(-m+4\right)=0\)
\(\Leftrightarrow9+4m-16=0\)
\(\Leftrightarrow7+4m=0\)
\(\Leftrightarrow m=-\frac{7}{4}\)
Vậy => m = -7/4
c, Ko rõ
PT
1
CM
18 tháng 3 2017
Điều kiện : x≥ 1
Pt
⇔ 3 x - 1 x + 1 + m = 2 x 2 - 1 4 ( x + 1 ) 2 4 ⇔ 3 x - 1 x + 1 + m = 2 x - 1 x + 1 4 t = x - 1 x + 1 4
với x ≥ 1 t a c ó 0 ≤ t < 1 .
Thay vào phương trình ta được m= 2t- 3t2= f(t)
Ta c ó đạo hàm f’ (t) = 2-6t ta có: f’ (t) =0 khi t= 1/3
Bảng biến thiên:
Từ bảng biến thiên ta có để phương trình có hai nghiệm khi 0≤ m <1/3.
Chọn D.
CM
8 tháng 9 2019
Chọn D
Điều kiện x ≥ 1
Ta có phương trình 3 x - 1 + m x + 1 = 2 x 2 - 1 4
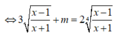
Đặt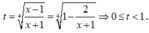 
Phương trình trở thành: 
Nhận xét: Mỗi giá trị của t ∈ [0;1) cho ta 1 nghiệm x ∈ [1;+ ∞ )
Do đó phương trình đã cho có 2 nghiệm thực phân biệt
⇔ phương trình (1) có nghiệm phân biệt t ∈ [0;1)
Bảng biến thiên:
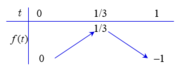
Từ bảng biến thiên suy ra 0 ≤ m < 1 3
20 tháng 6 2023
a: a*c<0
=>(1) có hai nghiệm phân biệt
b: Bạn viết lại biểu thức đi bạn
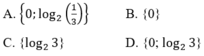
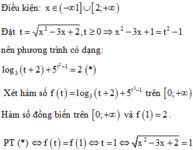
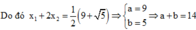
Lời giải:
Ta có công thức \(a^{\ln b}=b^{\ln a}\)
Thay \(a=3; b=2\Rightarrow 3^{\ln 2}=2^{\ln 3}\)
\(\Leftrightarrow 3=2^{\frac{\ln 3}{\ln 2}}\)
Do đó: \(3^x.2^{x^2}=1\)
\(\Leftrightarrow 2^{x.\frac{\ln 3}{\ln 2}}.2^{x^2}=1\)
\(\Leftrightarrow 2^{x^2+x.\frac{\ln 3}{\ln 2}}=1\)
\(\Leftrightarrow x^2+x.\frac{\ln 3}{\ln 2}=0\)
\(\Leftrightarrow x(x+\frac{\ln 3}{\ln 2})=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{\ln3}{\ln2}=-\log_23\end{matrix}\right.\)
Vậy \(x\in \left\{0; -\log_23\right\}\)