Cho nửa đường tròn (O) đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax tại C và cắt By tại D.
a) Chứng minh CD = AC + BD và góc COD = 90 độ.
b) AD cắt BC tại N. Chứng minh MN // BD
c) Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường...
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax tại C và cắt By tại D.
a) Chứng minh CD = AC + BD và góc COD = 90 độ.
b) AD cắt BC tại N. Chứng minh MN // BD
c) Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn
d) Gọi H là trung điểm của AM. CM: 3 điểm O, H, C thẳng hàng
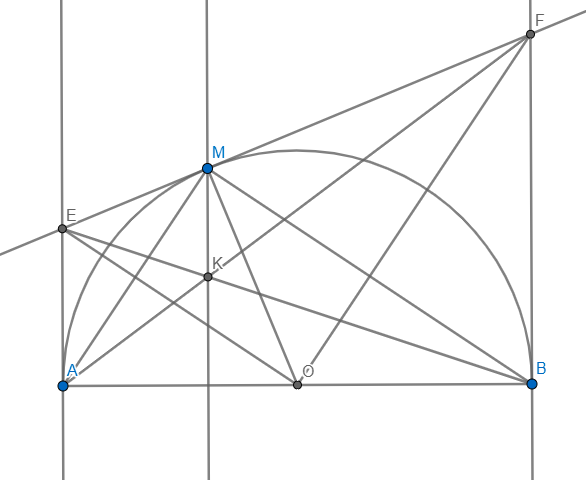
Cho nửa đường tròn (O) đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax tại C và cắt By tại D.
a) Chứng minh CD = AC + BD và góc COD = 90 độ.
b) AD cắt BC tại N. Chứng minh MN // BD
c) Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn
d) Gọi H là trung điểm của AM. CM: 3 điểm O, H, C thẳng hàn
a) Tiếp tuyến AC cắt tiếp tuyến CM tại C
\(\Rightarrow\) AC=CM và OC là phân giác của \(\widehat{MOA}\)
Tiếp tuyến BD cắt tiếp tuyến DM tại D
\(\Rightarrow\) BD=DM và OD là phân giác của \(\widehat{BOM}\)
Mặt khác: CD=CM+MC
\(\Leftrightarrow\) CD= AC+BD
Ta có: OC là phân giác của \(\widehat{MOA}\)
OD là phân giác của \(\widehat{BOM}\)
Mà \(\widehat{MOA}\) và \(\widehat{BOM}\) là hai góc kề bù
\(\Rightarrow\) \(\widehat{COD}=90^o\)
b) Ta có: \(AC\perp AB\)
\(BD\perp AB\)
\(\Rightarrow AC//BD\)
Xét \(\Delta BND\) có: AC//BD
\(\Rightarrow\dfrac{CN}{BN}=\dfrac{AC}{BD}\) ( hệ quả của định lí Ta-let)
Mà AC=CM và BD=MD
\(\Rightarrow\dfrac{CN}{BN}=\dfrac{CM}{MD}\)
Xét \(\Delta BCD\) có:
\(\dfrac{CN}{BN}=\dfrac{CM}{MD}\left(cmt\right)\)
\(\Rightarrow MN//BD\)
c) CD là tiếp tuyến của (O)
\(\Rightarrow OM\perp CD\) tại M
Áp dụng hệ thức về cạnh và đường cao trong \(\Delta COD\left(\widehat{COD}=90^o\right)\) ta được:
\(OM^2=CM.MD\Leftrightarrow R^2=CM.MD\)
Mặt khác: AC=MC và BD=MD
\(\Rightarrow R^2=AC.BD\) (không đổi)