Cho ΔABC vuông tại A .Đường cao AH ; có AB = 5cm , BC=13cm. Tính AC , CH , AH
Giải hộ mk vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 10 2021
Bài 2:
Xét ΔABC có AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)
\(\Leftrightarrow\dfrac{AB}{AC}=\dfrac{1}{3}\)
\(\Leftrightarrow\dfrac{BH}{CH}=\dfrac{1}{9}\)
13 tháng 1
Xét ΔAHB vuông tại H có \(tanB=\dfrac{AH}{HB}\)
=>\(\dfrac{2.4}{HB}=\dfrac{3}{4}\)
=>\(HB=2.4\cdot\dfrac{4}{3}=3,2\left(cm\right)\)
ΔABH vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(AB^2=3,2^2+2,4^2=16\)
=>\(AB=\sqrt{16}=4\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)
=>\(BC=\dfrac{4^2}{3,2}=5\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=5^2-4^2=9\)
=>\(AC=\sqrt{9}=3\left(cm\right)\)
Chu vi tam giác ABC là:
3+4+5=12(cm)
2 tháng 10 2021
Bài 2:
b: \(AH\cdot\left(\cot\widehat{B}+\cot\widehat{C}\right)\)
\(=AH\cdot\left(\dfrac{BH}{AH}+\dfrac{CH}{AH}\right)\)
\(=AH\cdot\dfrac{BC}{AH}=BC\)
14 tháng 10 2021
Xét tg AHC vg tại H: \(\sin\widehat{C}=\dfrac{AH}{AC}=\sin30^0=\dfrac{1}{2}\Leftrightarrow AC=4\)
Xét tg ABC vg tại A: \(\tan\widehat{C}=\tan30^0=\dfrac{AB}{AC}=\dfrac{\sqrt{3}}{3}\Leftrightarrow AB=\dfrac{4\sqrt{3}}{3}\)
2 tháng 10 2021
Bài 1:
a: Xét ΔBAC vuông tại A có
\(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=60^0\)
Xét ΔBAC vuông tại A có
\(AB=BC\cdot\sin60^0\)
\(\Leftrightarrow BC=4\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow AC=2\sqrt{3}\left(cm\right)\)
10 tháng 5 2022
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: ta có: ΔABC\(\sim\)ΔHBA
nên BA/BH=BC/BA
hay \(BA^2=BH\cdot BC\)
10 tháng 5 2022
a.Xét tam giác ABC và tam giác HBA, có:
^B: chung
^BAC = ^BHA = 90 độ
Vậy tam giác ABC đồng dạng tam giác HBA (g.g)
b.\(\rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\)
\(\Leftrightarrow AB^2=BH.BC\left(đfcm\right)\) (1)
c.Áp dụng định lý pitago \(\Rightarrow BC=\sqrt{6^2+10^2}=2\sqrt{34}\left(cm\right)\)
(1) \(\Leftrightarrow6^2=2\sqrt{34}BH\)
\(\Leftrightarrow BH=\dfrac{9\sqrt{34}}{17}\left(cm\right)\)
Áp dụng định lý pitago trong tam giác ABH \(\Rightarrow AH=\sqrt{6^2-\left(\dfrac{9\sqrt{34}}{17}\right)^2}=\dfrac{15\sqrt{34}}{17}\left(cm\right)\)
17 tháng 8 2021
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AB^2=81\)
hay AB=9cm
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
hay \(\widehat{B}=53^0\)
3 tháng 10 2021
\(a,AB=\sqrt{BC^2-AC^2}=9\left(cm\right)\)
\(b,\)Áp dụng HTL:
\(AH\cdot BC=AC\cdot AB\\ \Rightarrow AH=\dfrac{12\cdot9}{15}=7,2\left(cm\right)\)
Vì AD là p/g nên \(\dfrac{AB}{AC}=\dfrac{BD}{DC}=\dfrac{3}{4}\Rightarrow BD=\dfrac{3}{4}DC\)
Mà \(BD+DC=BC=15\Rightarrow\dfrac{5}{4}DC=15\Rightarrow DC=12\left(cm\right)\)
Áp dụng HTL: \(HC=\dfrac{AC^2}{BC}=9,6\left(cm\right)\)
\(\Rightarrow HD=CD-HC=2,4\left(cm\right)\)
Áp dụng pytago: \(AD=\sqrt{AH^2+DH^2}=\dfrac{12\sqrt{10}}{5}\left(cm\right)\)
H9
HT.Phong (9A5)
CTVHS
8 tháng 10 2023
Ta có:
\(sinC=\dfrac{AB}{BC}\Rightarrow sin30^o=\dfrac{AB}{5}\)
\(\Rightarrow AB=5\cdot sin30^o=\dfrac{5}{2}\left(cm\right)\)
Mà: \(tanC=\dfrac{AB}{AC}\Rightarrow tan30^o=\dfrac{\dfrac{5}{2}}{AC}\)
\(\Rightarrow AC=\dfrac{\dfrac{5}{2}}{tan30^o}=\dfrac{5\sqrt{3}}{2}\left(cm\right)\)
Theo hệ thức đường cao cạnh góc vuông và cạnh huyền ta có:
\(AB\cdot AC=AH\cdot BC\)
\(\Rightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{\dfrac{5}{2}\cdot\dfrac{5\sqrt{3}}{2}}{5}=\dfrac{5\sqrt{3}}{4}\left(cm\right)\)
Ta có: \(\left\{{}\begin{matrix}HB=\dfrac{AB^2}{BC}=\dfrac{\left(\dfrac{5}{2}\right)^2}{5}=\dfrac{5}{4}\left(cm\right)\\HC=\dfrac{AC^2}{BC}=\dfrac{\left(\dfrac{5\sqrt{3}}{2}\right)^2}{5}=\dfrac{15}{4}\left(cm\right)\end{matrix}\right.\)
KV
8 tháng 10 2023
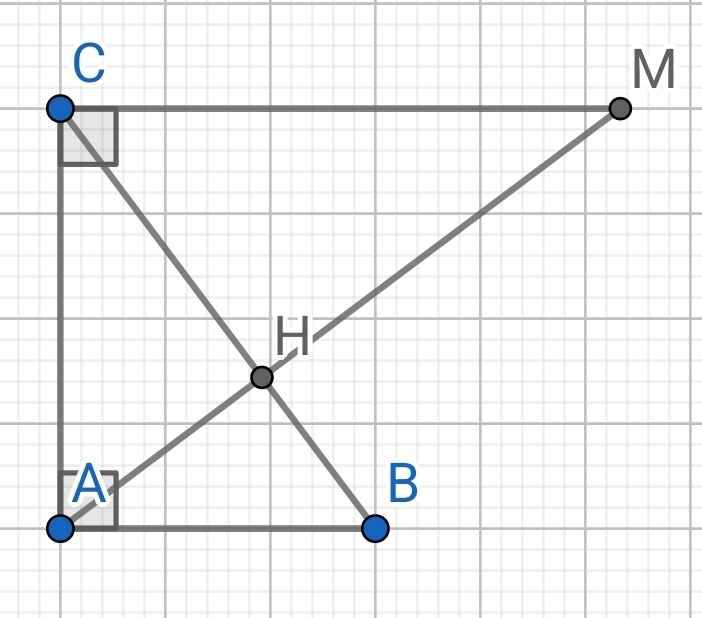a) ∠ABC = 90⁰ - 30⁰ = 60⁰
sinC = AB/BC
⇒ AB = BC.sinC
= 5.sin30⁰
= 5.1/2
= 5/2 (cm)
sinB = AC/BC
⇒ AC = BC.sinB
= 5.sin60⁰
= 5√3/2 (cm)
Ta có:
AH.BC = AB.AC
⇒ AH = AB.AC : BC
= 5/2 . 5√3/2 : 5
= 5√3/4 (cm)
AB² = BH.BC
⇒ BH = AB² : BC
= (5/2)² : 5
= 5/4 (cm)
⇒ CH = BC - BH
= 5 - 5/4
= 15/4 (cm)
b) Do AH ⊥ BC (gt)
⇒ CH ⊥ AM
∆ACM vuông tại C có CH là đường cao
⇒ AC² = AH . AM (1)
∆ABC vuông tại A có AH là đường cao
⇒ AC² = CH . CB (2)
Từ (1) và (2) ⇒ AH.AM = CH.CB
Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay AC=12(cm)
Xét ΔACB vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}CH=\dfrac{144}{13}\left(cm\right)\\AH=\dfrac{60}{13}\left(cm\right)\end{matrix}\right.\)
C.ơn bn nhìu nha