BT
Cho biểu thức : P =(1 phần x-1-x phần 1-3x^3 nhân x^2+x+1 phần x+1):(2x+1 phần x^2 +1)
a) điều kiện xác định P
b) Rút gọn biểu thức P
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 2:
a: Để (d1) cắt (d2) thì \(m-1\ne3-m\)
=>\(2m\ne4\)
=>\(m\ne2\)
b: Thay m=0 vào (d1), ta được:
\(y=\left(0-1\right)x+2=-x+2\)
Thay m=0 vào (d2), ta được:
\(y=\left(3-0\right)x-2=3x-2\)
Vẽ đồ thị:
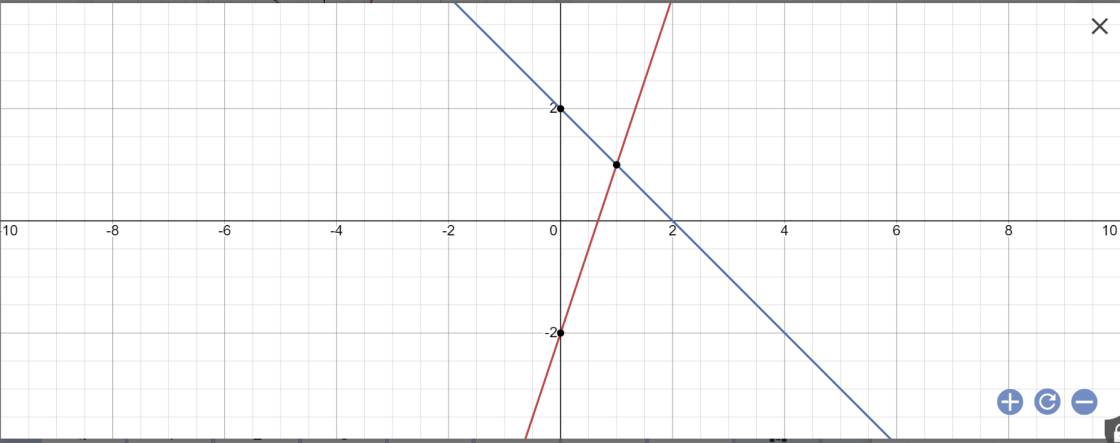
c: Phương trình hoành độ giao điểm là:
3x-2=-x+2
=>3x+x=2+2
=>4x=4
=>x=1
Thay x=1 vào y=3x-2, ta được:
y=3*1-2=3-2=1
d:
Khi m=0 thì (d2): y=3x-2
Gọi \(\alpha\) là góc tạo bởi (d2): y=3x-2 với trục Ox
y=3x-2 nên a=3
\(tan\alpha=a=3\)
=>\(\alpha\simeq72^0\)
Câu 3:
a: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM là đường trung trực của AB
=>OM\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2\)
=>\(OH\cdot OM=R^2\)
b: Ta có: AC//OM
OM\(\perp\)AB
Do đó: AB\(\perp\)AC
=>ΔABC vuông tại A
=>ΔABC nội tiếp đường tròn đường kính BC
mà ΔABC nội tiếp (O)
nên O là trung điểm của BC
=>B,O,C thẳng hàng
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>BE\(\perp\)EC tại E
=>BE\(\perp\)CM tại E
Xét ΔMBC vuông tại B có BE là đường cao
nên \(ME\cdot MC=MB^2\)(3)
Xét ΔMBO vuông tại B có BH là đường cao
nên \(MH\cdot MO=MB^2\left(4\right)\)
Từ (3) và (4) suy ra \(ME\cdot MC=MH\cdot MO\)

Bài 1.
a) ( x - 2)2 - ( x + 3)( x - 3)= 17
=> x2 - 4x + 4 - x2 + 9 - 17 = 0
=> -4x - 4 = 0
=> -4( x + 1 ) = 0
=> x = -1
Vậy,...
b)4( x - 3)2 - ( 2x - 1)( 2x + 1) = 10
=> 4( x2 - 6x + 9) - 4x2 + 1 - 10 = 0
=> - 24x + 36 - 9 = 0
=> -24x + 27 = 0
=> -3( 8x - 9) = 0
=> x = \(\dfrac{9}{8}\)
Vậy,...
c) ( x - 4)2 - ( x - 2)( x + 2)= 36
=> x2 - 8x + 16 - x2 + 4 - 36 = 0
=> -8x - 16 = 0
=> -8( x + 2) = 0
=> x = -2
d) ( 2x + 3)2 - ( 2x + 1)( 2x - 1) = 10
=> 4x2 + 12x + 9 - 4x2 + 1 - 10 = 0
=> 12x = 0
=> x = 0
Vậy,...
Bài 2.
\(\dfrac{3x^2+3x}{\left(x+1\right)\left(2x-6\right)}\)
a) ĐKXĐ : ( x + 1)( 2x - 6) # 0
=> 2( x + 1)( x - 3) # 0
=> x # -1 ; x # 3
Vậy,...
b) Để P = 1
=> \(\dfrac{3x^2+3x}{\left(x+1\right)\left(2x-6\right)}=1\)
=> \(\dfrac{3x\left(x+1\right)}{2\left(x+1\right)\left(x-3\right)}=\dfrac{3x}{2\left(x-3\right)}=1\)
=> 3x = 2x - 6
=> x = -6 ( thỏa mãn ĐKXĐ)
Vậy,...
Bài 3.
P = \(\dfrac{x}{x-1}+\dfrac{x^2+1}{1-x^2}\)
a) Để P có nghĩa tức P xác định .
ĐKXĐ : x - 1 # 0 => x # 1
* 1 - x2 # 0 => x # 1 ; x # -1
Vậy,...
b) P = \(\dfrac{x}{x-1}+\dfrac{x^2+1}{1-x^2}\)
P = \(\dfrac{x^2+x-x^2-1}{\left(x-1\right)\left(x+1\right)}=\dfrac{x-1}{\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x+1}\)( x# 1; x# -1)
c) Để P = -1 thì :
\(\dfrac{1}{x+1}=-1\)
=> -x - 1 = 1
=> x = -2 ( thỏa mãn ĐKXĐ )
Vậy,...

\(B=\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right)\cdot\dfrac{\left(1-x\right)^2}{2}\)
a) ĐK: \(x\ne1,x\ge0\)
\(B=\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right)\cdot\dfrac{\left(1-x\right)^2}{2}\)
\(B=\left[\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}\right]\cdot\dfrac{\left(x-1\right)^2}{2}\)
\(B=\left[\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}\right]\cdot\dfrac{\left(x-1\right)^2}{2}\)
\(B=\left[\dfrac{x+\sqrt{x}-2\sqrt{x}-2-x+\sqrt{x}-2\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}\right]\cdot\dfrac{\left(x-1\right)^2}{2}\)
\(B=\dfrac{-2\sqrt{x}}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)^2}{2}\)
\(B=-\sqrt{x}\left(\sqrt{x}-1\right)\)

a, ĐKXĐ: \(\hept{\begin{cases}x^3+1\ne0\\x^9+x^7-3x^2-3\ne0\\x^2+1\ne0\end{cases}}\)
b, \(Q=\left[\left(x^4-x+\frac{x-3}{x^3+1}\right).\frac{\left(x^3-2x^2+2x-1\right)\left(x+1\right)}{x^9+x^7-3x^2-3}+1-\frac{2\left(x+6\right)}{x^2+1}\right]\)
\(Q=\left[\frac{\left(x^3+1\right)\left(x^4-x\right)+x-3}{\left(x+1\right)\left(x^2-x+1\right)}.\frac{\left(x-1\right)\left(x+1\right)\left(x^2-x+1\right)}{\left(x^7-3\right)\left(x^2+1\right)}+1-\frac{2\left(x+6\right)}{x^2+1}\right]\)
\(Q=\left[\left(x^7-3\right).\frac{\left(x-1\right)}{\left(x^7-3\right)\left(x^2+1\right)}+1-\frac{2\left(x+6\right)}{x^2+1}\right]\)
\(Q=\frac{x-1+x^2+1-2x-12}{x^2+1}\)
\(Q=\frac{\left(x-4\right)\left(x+3\right)}{x^2+1}\)

a: \(A=\left(\dfrac{x}{x^2-4}+\dfrac{4}{x-2}+\dfrac{1}{x+2}\right):\dfrac{3x+3}{x^2+2x}\)
\(=\dfrac{x+4x+8+x-2}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x\left(x+2\right)}{3\left(x+1\right)}\)
\(=\dfrac{6\left(x+1\right)\cdot x\left(x+2\right)}{3\left(x+1\right)\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x}{x-2}\)