cho ΔABC có góc A=90o, AB<AC.Gọi M là trung điểm BC. Từ M kẻ MN ⊥BC (C ϵ AC). TRên tia đối AC lấy I sao cho AI=AN BI cắt AM tại H
a) cm: AM= 1/2BC
b)∠AMB=∠ANB
c)cm: BH=AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(\dfrac{AB}{5}=\dfrac{AC}{12}\)
\(\Rightarrow\dfrac{AB^2}{25}=\dfrac{AC^2}{144}=\dfrac{AB^2+AC^2}{25+144}=\dfrac{BC^2}{169}=4\)
\(\Rightarrow\left\{{}\begin{matrix}AB=10\\AC=24\end{matrix}\right.\) ( cm )
- Áp dụng hệ thức lượng vào tam giác ABC vuông tại A đường cao AH .
\(AH.BC=AB.AC\)
\(\Rightarrow AH=\dfrac{120}{13}\left(cm\right)\)
- Áp dụng định lý pitago vào tam giác ABH vuông tại H :
\(BH=\sqrt{AB^2-AH^2}=\dfrac{50}{13}\left(cm\right)\)
- Áp dụng định lý pitago vào tam giác ACH vuông tại H :
\(CH=\sqrt{AC^2-AH^2}=\dfrac{288}{13}\left(cm\right)\)
Vậy ..

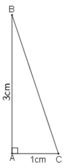
- Vẽ góc ∠ xAy = 90º
- Trên tia Ax lấy điểm B sao cho AB = 3cm.
Trên tia Ay lấy điểm C sao cho AC = 1cm.
- Nối các điểm B và C ta được tam giác ABC thỏa mãn.
Đo góc C ta được ∠C ≈ 72o.

Lời giải:
a. Xét tam giác $ABH$ và $ACK$ có:
$AB=AC$
$\widehat{A}$ chung
$\widehat{AHB}=\widehat{AKC}=90^0$
$\Rightarrow \triangle ABH=\triangle ACK$ (ch-gn)
$\Rightarrow AH=AK$
b.
Từ tam giác bằng nhau phần a suy ra $\widehat{B_1}=\widehat{C_1}$
Vì $AB=AC; AK=AH\Rightarrow AB-AK=AC-AH$
$\Rightarrow BK=CH$
Xét tam giác $KBI$ và $HCI$ có:
$\widehat{B_1}=\widehat{C_1}$
$\widehat{BKI}=\widehat{CHI}=90^0$
$BK=CH$
$\Rightarrow \triangle KBI=\triangle HCI$ (c.g.c)
$\Rightarrow BI=CI$
Xét tam giác $ABI$ và $ACI$ có:
$AB=AC$
$AI$ chung
$BI=CI$
$\Rightarrow \triangle ABI=\triangle ACI$ (c.c.c)
$\Rightarrow \widehat{BAI}=\widehat{CAI}$
$\Rightarrow AI$ là phân giác $\widehat{A}$
$

ta có: tan B=\(\dfrac{8}{15}\)
=>tan B=\(\dfrac{8}{15}=\dfrac{AC}{AB}\)
mà AB=30 cm (gt)
=> AC= 8.30:15=16 cm
xét tam giác ABC vuông tại A (gt)
=> AC2+AB2=BC2 ( Định lí pytago)
hay 162+302=BC2
=>BC=\(\sqrt{16^2+30^2}=34\)
ta có sin B=\(\dfrac{AC}{CB}=\dfrac{16}{34}=\dfrac{8}{17}\)
cos B= \(\dfrac{AB}{BC}=\dfrac{30}{34}=\dfrac{15}{17}\)
cotg B =\(\dfrac{30}{16}=\dfrac{15}{8}\)

- Áp dụng định lý pitago vào tam giác ABC vuông tại A .
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=20\left(cm\right)\)
- Áp dụng hệ thức lượng vào tam giác ABC đường cao AH .
\(AH.BC=AB.AC\)
\(\Rightarrow AH=9,6\left(cm\right)\)
- Áp dụng định lý pitago vào tam giác ABH vuông tại H :
\(BH=\sqrt{AB^2-AH^2}=7,2\left(cm\right)\)
- Áp dụng định lý pitago vào tam giác ACH vuông tại H :
\(CH=\sqrt{AC^2-AH^2}=12,8\left(cm\right)\)
Ta có : AD là đường phân giác của tam giác ABC .
\(\Rightarrow\dfrac{AB}{BD}=\dfrac{AC}{CD}=\dfrac{AB+AC}{BD+CD}=\dfrac{AB+AC}{BC}=1,4\)
=> BD = 60/7 (cm )
=> HD = BD - BH = 48/35 (cm ) .

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow CH=\dfrac{12^2}{9}=\dfrac{144}{9}=16\left(cm\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{AH\cdot BC}{2}=\dfrac{12\cdot25}{2}=\dfrac{300}{2}=150\left(cm^2\right)\)

a) Xét ΔACE vuông tại C và ΔAKE vuông tại K có
AE chung
\(\widehat{CAE}=\widehat{KAE}\)(AE là tia phân giác của \(\widehat{CAK}\))
Do đó: ΔACE=ΔAKE(Cạnh huyền-góc nhọn)
Suy ra: AC=AK(Hai cạnh tương ứng)

Xét ΔAIK vuông tại K và ΔAIH vuông tại H có:
AH = AK (theo phần a)
AI chung
⇒ ΔAIK = ΔAIH (cạnh huyền – cạnh góc vuông).
⇒ góc IAK = góc IAH (hai góc tương ứng)
Vậy AI là tia phân giác của góc A.

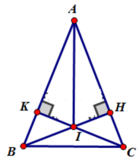

Xét ΔABH vuông tại H và ΔACK vuông tại K có:
AB = AC (Do ΔABC cân tại A)
góc A chung
Nên ΔABH = ΔACK (cạnh huyền – góc nhọn) ⇒ AH = AK (hai cạnh tương ứng).