Cho hình thang cân ABCD ( ab//cd) có góc A = góc 3D . tính các góc của hình thang cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tương tự bài 1A. Ta có: C ^ = D ^ = 45 0 , A ^ = B ^ = 135 0

Bài 6:
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{ACD}\)
nên \(\widehat{ACB}=\widehat{ACD}\)
hay CA là tia phân giác của \(\widehat{BCD}\)

Bài 3:
Xét ΔACD và ΔBDC có
AC=BD
CD chung
AD=BC
Do đó: ΔACD=ΔBDC
Suy ra: \(\widehat{ACD}=\widehat{BDC}\)
hay \(\widehat{OCD}=\widehat{ODC}\)
Xét ΔODC có \(\widehat{OCD}=\widehat{ODC}\)
nên ΔODC cân tại O
Suy ra: OD=OC
Ta có: AO+OC=AC
OB+OD=BD
mà AC=BD
và OC=OD
nên OA=OB
Bài 2:
Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔAHB=ΔAKC
Suy ra: AH=AK và HB=KC
Xét ΔABC có
\(\dfrac{AK}{AB}=\dfrac{AH}{HC}\)
Do đó: KH//BC
Xét tứ gác BKHC có KH//BC
nên BKHC là hình thang
mà KC=BH
nên BKHC là hình thang cân

Bài 2:
Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔAHB=ΔAKC
Suy ra: AH=AK
Xét ΔABC có
\(\dfrac{AK}{AB}=\dfrac{AH}{AC}\)
Do đó: HK//BC
Xét tứ giác BCHK có HK//BC
nên BCHK là hình thang
mà HB=KC(ΔAHB=ΔAKC)
nên BCHK là hình thang cân
Bài 3:
Xét ΔACD và ΔBDC có
AC=BD
CD chung
AD=BC
Do đó: ΔACD=ΔBDC
Suy ra: \(\widehat{ACD}=\widehat{BDC}\)
hay \(\widehat{OCD}=\widehat{ODC}\)
Xét ΔODC có \(\widehat{OCD}=\widehat{ODC}\)
nên ΔODC cân tại O
Suy ra: OD=OC
Ta có: AO+OC=AC
OB+OD=BD
mà AC=BD
và OC=OD
nên OA=OB

Bafi1: Do AB // CD ( GT )
⇒ˆA+ˆC=180o
⇒2ˆC+ˆC=180o
⇒3ˆC=180o
⇒ˆC=60o
⇒ˆA=60o.2=120o
Do ABCD là hình thang cân
⇒ˆC=ˆD
Mà ˆC=60o
⇒ˆD=60o
AB // CD ⇒ˆD+ˆB=180o
⇒ˆB=180o−60o=120o
Vậy ˆA=ˆB=120o;ˆC=ˆD=60o
Bài 2:
Ta có; AB//CD
\(\Rightarrow\)góc BAD+ góc ADC= \(180^o\)
^A=3. ^D \(\Rightarrow\)\(\dfrac{A}{3}\)=^D
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\dfrac{A}{3}=\dfrac{D}{1}=\dfrac{A+D}{3+1}=\dfrac{180^O}{4}=45^O\)
\(\Rightarrow\)^A= \(135^O\)
\(\Rightarrow\)^D=\(45^o\)
\(\Rightarrow B=A=135^o\)
\(\Rightarrow C=D=45^o\)

Vì ABCD là htc nên \(\widehat{A}=2\widehat{C}=2\widehat{D}\)
Mà AB//CD nên \(\widehat{A}+\widehat{D}=180^0\Rightarrow3\widehat{D}=180^0\Rightarrow\widehat{D}=60^0\Rightarrow\widehat{A}=120^0\)
Vì ABCD là htc nên \(\widehat{A}=\widehat{B}=120^0;\widehat{D}=\widehat{C}=60^0\)

Bài 2:
a: Xét ΔABC có
\(\dfrac{BM}{AB}=\dfrac{CN}{AC}\)
Do đó: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân
b: Ta có: \(\widehat{B}=\widehat{C}=\dfrac{180^0-40^0}{2}=70^0\)
\(\widehat{BMN}=\widehat{CNM}=180^0-70^0=110^0\)

Bài 5:
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{ACD}\)
nên \(\widehat{ACB}=\widehat{ACD}\)
hay CA là tia phân giác của \(\widehat{BCD}\)

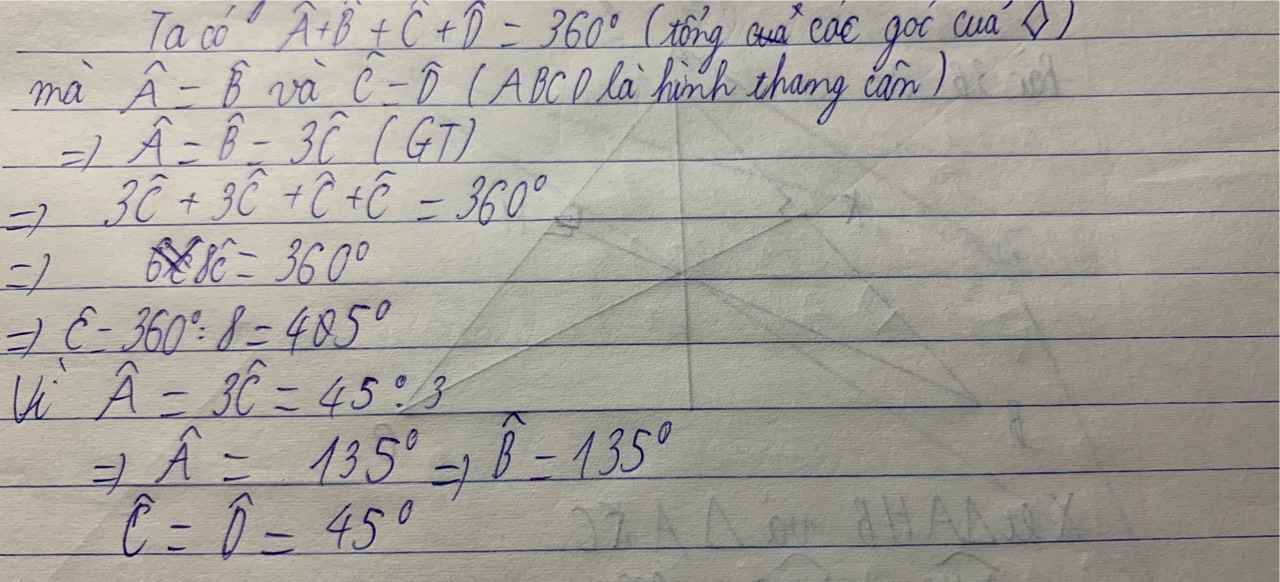
Ta có: \(\widehat{A}+\widehat{D}=180^o\)
Mà \(\widehat{A}=3\widehat{D}\)
\(\Rightarrow\widehat{A}=135^o;\widehat{D}=45^o\)
Ta có:\(\widehat{A}=\widehat{B}\);\(\widehat{C}=\widehat{D}\)