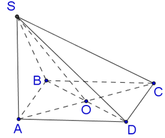
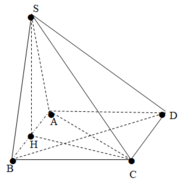
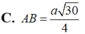Cho hình thoi ABCD có góc BAC=60o,với SABCD=\(2\sqrt{3}\)cm2.Tính AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B.
* Hướng dẫn giải:
Ta có

Mặt khác
![]()
![]()
Ta có:
S A B C D = 1 2 A C . B D = 2 a 2 3
⇒ V S . A B C D = 1 3 S H . S A B C D = 4 a 3 39 9

Đáp án là C
Gọi H là hình chiếu của A’ trên (ABCD). Dễ thấy góc
![]()
![]()
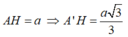
Dễ dàng tính được diện tích đáy

![]()

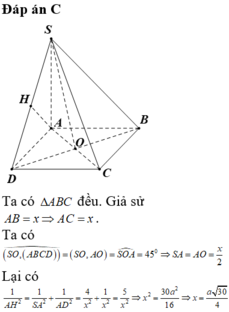
Đáp án C

Gọi E và H lần lượt là hình chiếu của A lên CB và SE
Ta có: A E = A B sin A B E ^ = s i n 60 ° = a 3 2
A H = A E sin 60 ° = 3 2 a . 3 2 = 3 a 4

a: \(SA=\sqrt{\left(\dfrac{a}{2}\right)^2\cdot2}=\sqrt{2}\cdot\dfrac{a}{\sqrt{2}}=a\)
\(SB=SA=a\)
AH=a/2; AD=a; góc A=120 độ
=>\(cosA=\dfrac{\dfrac{1}{4}a^2+a^2-DH^2}{2\cdot\dfrac{1}{2}a\cdot a}\)
=>\(\dfrac{5}{4}a^2-HD^2=a^2\cdot\dfrac{-1}{2}=\dfrac{-1}{2}a^2\)
=>HD^2=7/4a^2
=>\(HD=\dfrac{a\sqrt{7}}{2}\)
\(SD=\sqrt{SH^2+HD^2}=\sqrt{\dfrac{7}{4}a^2+\dfrac{1}{4}a^2}=a\sqrt{2}\)
Vì SA^2+AD^2=SD^2 và AS=AD
nên ΔASD vuôg cân tại A
(SD;BC)=(DS;DA)=góc SDA=45 độ