(*= độ)
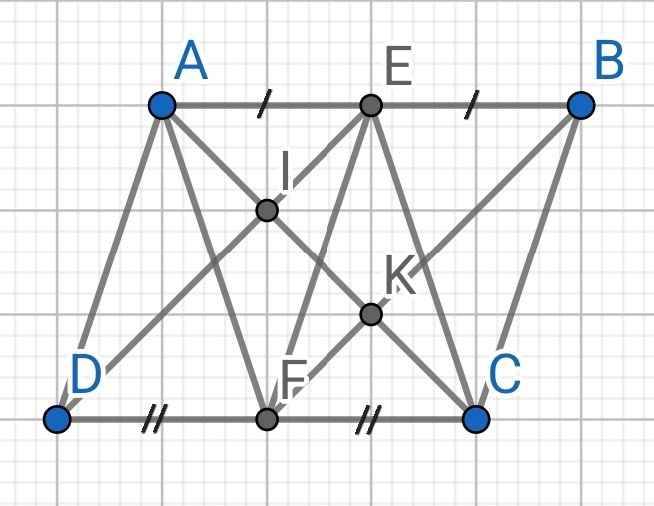
cho hình bình hành ABCD có A=60* , BC gấp 2 lần AB, E là trung điểm của BC , F là trung điểm của AD
a/ chứng minh ABEF là hình Thoi
b/ Chứng minh ABED là hình Thang cân
c/ tính số đo góc AED
d/ Lấy K đối xứng với A qua B chứng minh K đói xứng với D qua E

a: Xét tứ giác ABEF có
AF//BE
AF=BE
Do đó: ABEF là hình bình hành
mà AF=AB
nên ABEF là hình thoi
b: Xét ΔCDE có CD=CE
nên ΔCDE cân tại C
mà \(\widehat{C}=60^0\)
nên ΔCDE đều
=>\(\widehat{DEC}=60^0\)
=>\(\widehat{DEB}=\widehat{B}\)(=120 độ)
Xét tứ giác ABED có AD//BE
nên ABED là hình thang
mà \(\widehat{DEB}=\widehat{ABE}\)
nên ABED là hình thang can
c: Xét ΔAED có
EF là đường trung tuyến
EF=AD/2
Do đó: ΔAED vuông tại E
hay \(\widehat{AED}=90^0\)