K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1 2021
Do trắc nghiệm nên ta chỉ cần xét trường hợp đặc biệt nhất: đường thẳng này đi qua B, khi đó M trùng B và N là trung điểm AC
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AB}.\overrightarrow{AC}\)
Đồng thời do \(\overrightarrow{MB}=\overrightarrow{0}\) và \(\overrightarrow{NC}=\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AC}\) nên đáp án D đúng
NN
1
6 tháng 1 2016
hình tự vẽ nha bn! gọi K,I,P lần lượt là tđ của AB,AC,BC
ta có AG/AP=2/3=> S AMG/ABP=2/3=> AM/AB=2/3
ta có AM/AB=2/3,AG/AP=2/3=> MG//BP (định lý talet đảo)
khi MG//BP=> AB/AM=AP/AG (1)
khi GN//PC (MG//BP) => AP/AG=AC/AN (2)
từ (1),(2)=> AB/AM+AC/AN=2AP/AG=2.3/2=3
20 tháng 7 2023
Bài này có nhiều cách làm, vẽ thêm đường phụ cũng được, dùng định lý Menelaus cũng được nhưng lớp 10 thì nên dùng vecto
Ta có:
\(k=\dfrac{AG}{AB}=1-\dfrac{BG}{AB}=1-\dfrac{DE}{AB}=1-\dfrac{2DE}{3EF}\)
Đặt \(\dfrac{AD}{AM}=m\)
\(\Rightarrow\overrightarrow{ED}=m\overrightarrow{EM}+\left(1-m\right)\overrightarrow{EA}\)
\(=m\left(\overrightarrow{EC}+\overrightarrow{CM}\right)+\dfrac{1}{3}\left(m-1\right)\overrightarrow{AC}\)
\(=\dfrac{2}{3}m\overrightarrow{AC}+\dfrac{1}{2}m\overrightarrow{CB}+\dfrac{1}{3}\left(m-1\right)\overrightarrow{AC}\)
\(=\left(m-\dfrac{1}{3}\right)\overrightarrow{AC}+\dfrac{1}{2}m\overrightarrow{CB}\)
Lại có: \(\overrightarrow{EF}=\dfrac{2}{3}\overrightarrow{AB}=\dfrac{2}{3}\overrightarrow{AC}+\dfrac{2}{3}\overrightarrow{CB}\)
Mà \(D,E,F\) thẳng hàng nên:
\(\left(m-\dfrac{1}{3}\right)\dfrac{2}{3}=\dfrac{1}{2}m.\dfrac{2}{3}\Leftrightarrow m=\dfrac{2}{3}\)
\(\Rightarrow\overrightarrow{ED}=\dfrac{1}{2}\overrightarrow{EF}\Rightarrow ED=\dfrac{1}{2}EF\)\(\Leftrightarrow\dfrac{DE}{EF}=\dfrac{1}{2}\)
\(\Rightarrow k=\dfrac{2}{3}\)
H9
HT.Phong (9A5)
CTVHS
16 tháng 1
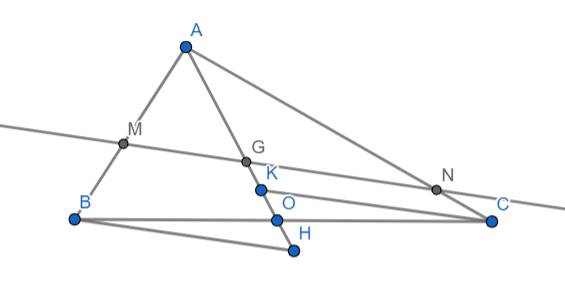
Xét 2 tam giác AMG và ABH ta có:
\(\widehat{BAH}\) chung
\(\widehat{AMG}=\widehat{ABH}\) (cặp góc đồng vị do BH//MG)
\(\Rightarrow\Delta AMG\sim\Delta ABH\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{AH}{AG}\) (1)
Xét 2 tam giác ANG và ACK có:
\(\widehat{CAK}\) chung
\(\widehat{ANG}=\widehat{ACK}\) (cặp góc đồng vị do CK//GN)
\(\Rightarrow\Delta ANG\sim\Delta ACK\left(g.g\right)\)
\(\Rightarrow\dfrac{AC}{AN}=\dfrac{AK}{AG}\) (2)
Xét hai tam giác BOH và COK ta có:
\(\widehat{BOH}=\widehat{COK}\) (đối đỉnh)
\(BO=CO\) (AO là đường trung tuyến nên O là trung điểm của BC)
\(\widehat{HBO}=\widehat{KCO}\) (so le trong vì BH//MN và CK//MN ⇒ BH//CK)
\(\Rightarrow\Delta BOH=\Delta COK\left(g.c.g\right)\)
\(\Rightarrow HO=OK\) (hai cạnh t.ứng)
\(\Rightarrow HK=2HO\)
Ta lấy (1) + (2) \(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{AH+AK}{AG}=\dfrac{AH+AH+HK}{AG}=\dfrac{2AH+HK}{AG}\)
\(=\dfrac{2AH+2HO}{AG}=\dfrac{2\left(AH+HO\right)}{AG}=\dfrac{2AO}{AG}\)
Mà G là trọng tâm của tam giác ABC \(\Rightarrow AO=\dfrac{3}{2}AG\)
\(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{2\cdot\dfrac{3}{2}AG}{AG}=2\cdot\dfrac{3}{2}=3\left(đpcm\right)\)