cho hình thang vuông abcd có góc a = b = 90 , ab = 4cm , bc = 13 cm , cd = 9cm .
tính ad
chứng minh ad là tiếp tuyến đường tròn đường kính bc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 3 2019
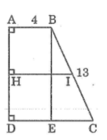
Gọi I là trung điểm của BC
Ta có: IB = IC = (1/2).BC = (1/2).13 = 6,5 (cm) (1)
Kẻ IH ⊥ AD. Khi đó HI là đường trung bình của hình thang ABCD.
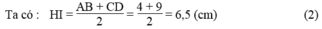
Từ (1) và (2) suy ra : IB = IH = R
Vậy đường tròn (I ; BC/2 ) tiếp xúc với đường thẳng AD
23 tháng 11 2015
a) Kẻ BH vg với CD.
ABHD là HCN nên AD = BH .
Theo định lí py - ta - go:
\(AD=BH=\sqrt{BC^2-CH^2}=\sqrt{13^2-\left(9-4\right)^2}=12\)
b) O ở đâu vậy
4 tháng 9 2019
a. Kẻ BE ⊥ CD
Suy ra tứ giác ABED là hình chữ nhật
Ta có: AD = BE
AB = DE = 4 (cm)
Suy ra: CE = CD – DE = 9 – 4 = 5 (cm)
Áp dụng định lí Pitago vào tam giác vuông BCE ta có :
BC2 = BE2 + CE2
Suy ra : BE2 = BC2 – CE2 = 132 – 52 = 144
BE = 12 (cm)
Vậy: AD = 12 (cm)
b. Gọi I là trung điểm của BC
Ta có: IB = IC = (1/2).BC = (1/2).13 = 6,5 (cm) (1)
Kẻ IH ⊥ AD. Khi đó HI là đường trung bình của hình thang ABCD.
Từ (1) và (2) suy ra : IB = IH = R
Vậy đường tròn (I ; BC/2 ) tiếp xúc với đường thẳng AD
2 tháng 8 2020
a. Kẻ \(BE\perp CD\)
Suy ra tứ giác ABED là hình chữ nhật
Ta có: AD = BE
AB = DE = 4 ( cm )
Suy ra: CE = CD – DE = 9 – 4 = 5 ( cm )
Áp dụng định lí Pitago vào tam giác vuông BCE ta có :
BC2 = BE2 + CE2
Suy ra : BE2 = BC2 – CE2 = 132 – 52 = 144
BE = 12 ( cm )
Vậy: AD = 12 ( cm )
b. Gọi I là trung điểm của BC
Ta có: \(IB=IC=\left(\frac{1}{2}\right).BC=\left(\frac{1}{2}\right).13=6,5\left(cm\right)\left(1\right)\)
Kẻ \(IH\perp AD\). Khi đó HI là đường trung bình của hình thang ABC
Ta có : \(HI=\frac{AB+CD}{2}=\frac{4+9}{2}=6,5\left(cm\right)\left(2\right)\)
Từ (1) và (2) suy ra : IB = IH = R
Vậy đường tròn \(\left(I;\frac{BC}{2}\right)\) tiếp xúc với đường thẳng AD