1)Cho tam giác ABC có\(\widehat{A}=50^0;\widehat{B}=20^0\).Trên phân giác BE lấy F sao cho \(\widehat{FAB}=20^0\) .I là trung điểm AF, K là giao điểm cua EI và AB.Tính \(\widehat{KCB}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
27 tháng 2 2020
Gọi H là trung điểm của AC. \(\Delta\)DAC cân tại D.
Do đó DH\(\perp\)AC và AH = \(\frac{1}{2}\)AC (1)
Vẽ AK \(\perp\)BC. Vì \(\Delta\)AKC vuông tại K và ^BCA = 300
nên AK = \(\frac{1}{2}\)AC (2)
Từ (1) và (2) suy ra AK = AH
Xét \(\Delta\)AKB và \(\Delta\)AHD có:
^AKB = ^AHD (=900)
AK = AH(gt)
^BAK = ^DAH (=500)
Do đó \(\Delta\)AKB = \(\Delta\)AHD (g.c.g)
=> AB = AD
Vậy \(\Delta\)ABD cân tại A(đpcm)
12 tháng 1 2022
\(\widehat{B}+\widehat{C}=140^0\)
\(\Leftrightarrow4\cdot\widehat{C}=140^0\)
\(\Leftrightarrow\widehat{C}=35^0\)
hay \(\widehat{B}=105^0\)
Vậy: ΔABC tù
17 tháng 9 2023
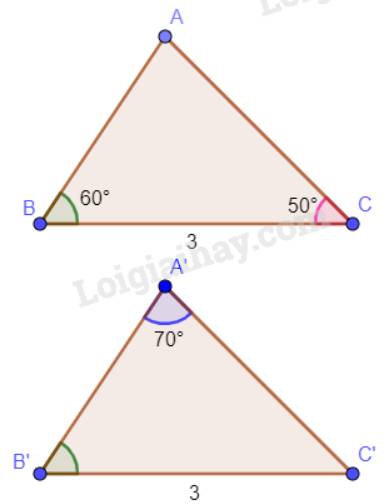
Tổng ba góc trong một tam giác bằng 180°. Vậy trong tam giác A’B’C’ có \(\widehat {C'} = 180^\circ - 70^\circ - 60^\circ = 50^\circ \).
Xét hai tam giác ABC và A’B’C’ có:
\(\widehat B = \widehat {B'} = 60^\circ ;\)
BC = B’C’ ( = 3 cm)
\(\widehat C = \widehat {C'} = 50^\circ \)
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
Q
15 tháng 10 2017
a)
A B C 100*
=> Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}\) = 180o
100o + \(\widehat{B}+\widehat{C}\) = 180o
\(\widehat{B}+\widehat{C}\) = 180o - 100o
\(\widehat{B}+\widehat{C}\) = 80o
Góc B = (80o+50o):2 = 65o
=> \(\widehat{C}\) = 65o - 50o = 15o
Vậy \(\widehat{B}\) = 65o ; \(\widehat{C}\) = 15o
b)
80* A B C
Ta có : \(\widehat{3A}+\widehat{B}+\widehat{2C}\) = 180o
\(\widehat{3A}+\widehat{2C}\) = 180o - 80o
\(\widehat{3A}+\widehat{2C}\) = 100o
=> \(\widehat{A}\) = 100o:(3+2).3 = 60o
\(\widehat{C}\) = 100o - 60o = 40o
Vậy \(\widehat{A}\) = 60o ; \(\widehat{C}\) = 40o
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Do \(\widehat{A}=100^0>90^0\) nên là góc tù, do đó, \(\widehat{A}\) là góc lớn nhất trong tam giác ABC.
\( \Rightarrow \) BC là cạnh lớn nhất của tam giác ABC (do BC đối diện với góc A trong tam giác ABC)
b)
Theo định lí tổng 3 góc trong tam giác ABC, ta có:
\( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat C = {180^o} - {100^o} - {40^o} = {40^o}\)
\( \Rightarrow\widehat C = \widehat B = {40^o}\)
\( \Rightarrow \) ABC là tam giác cân tại A.
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Theo đề bài ta có AB = 4cm, BC = 7cm, AC = 6cm
Có góc đối diện với cạnh AB là góc C, góc A đối diện với cạnh BC, góc B đối diện với cạnh AC
Theo định lí về góc đối diện với cạnh lớn hơn thì lớn hơn ta có :
\( \Rightarrow \widehat A > \widehat B > \widehat C\)
b)
Vì \(\widehat{A}=\widehat{C}\) nên tam giác ABC cân tại B
\( \Rightarrow BA = BC\)
Áp dụng định lí tổng 3 góc trong tam giác ABC, có:
\( \Rightarrow \widehat B = {180^o} - {100^0} = {80^o}\)
\( \Rightarrow \widehat B > \widehat A=\widehat C\)
\( \Rightarrow AC\) là cạnh lớn nhất tam giác ABC (Quan hệ giữa góc và cạnh đối diện trong tam giác)
NT
0
Trần Quốc LộcKien NguyenTrần Thị HưTRẦN MINhattori heijiH HOÀNGơngTrần Đăng hHPhạm Hoàng Giangung Ribi Nkok Ngoknguyenattori heijiNhấtAn Nguyễn Bá
đừng có nhắc đến tui chứ. Làm sao mà làm nổi bài này!