chứng minh rằng: x-x2-1<0 với mọi số thực thuộc x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
\(x^2-x+1\)
\(=x^2-2\cdot\dfrac{1}{2}\cdot x+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Mà: \(\left(x-\dfrac{1}{2}\right)^2\ge0\forall x\) và \(\dfrac{3}{4}>0\)
Nên: \(x^2-x+1>0\)
\(x^2-x+1\)
\(=x^2-\dfrac{1}{2}.x-\dfrac{1}{2}.x+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=x\left(x-\dfrac{1}{2}\right)-\dfrac{1}{2}\left(x-\dfrac{1}{2}\right)+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)\left(x-\dfrac{1}{2}\right)+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\) với mọi x ( đpcm )

a) Đề sai thì phải.Phải là CM: \(x^2-x+1>0\) với mọi x
Ta có:
\(x^2-x+1=\left(x^2-x+\frac{1}{4}\right)+\frac{3}{4}\)
\(=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\)
Vì \(\left(x-\frac{1}{2}\right)^2\ge0\) nên \(\left(x-\frac{1}{2}\right)^2+\frac{3}{4}>0\)
Vậy \(x^2-x+1>0\) với mọi \(x\in R\)
b)Ta có:
\(-x^2+2x-4=-\left(x^2-2x+1\right)-3\)
\(=-\left(x-1\right)^2-3\)
Vì \(-\left(x-1\right)^2\le0\) với mọi x nên \(-\left(x-1\right)^2-3< 0\)
Vậy \(-x^2+2x-4< 0\) với mọi \(x\in R\)

Ta có : x2 - 2xy + y2 + 1 = (x - y)2 + 1
Vì : \(\left(x-y\right)^2\ge0\forall x\in R\)
Nên : \(\left(x-y\right)^2+1\ge1\forall x\in R\)
Suy ra : \(\left(x-y\right)^2+1>0\forall x\in R\)
Vậy x2 - 2xy + y2 + 1 \(>0\forall x\in R\)
Ta có : x - x2 - 1
= -(x2 - x + 1)
\(=-\left(x^2-x+\frac{1}{4}+\frac{3}{4}\right)\)
\(=-\left(x^2-x+\frac{1}{4}\right)-\frac{3}{4}\)
\(=-\left(x-\frac{1}{2}\right)^2-\frac{3}{4}\)
Vì : \(-\left(x-\frac{1}{2}\right)^2\le0\forall x\in R\)
Nên : \(-\left(x-\frac{1}{2}\right)^2-\frac{3}{4}\le-\frac{3}{4}< 0\)
Vậy x - x2 - 1 \(< 0\forall x\in R\)

\(x^2-2xy+y^2+1\)
\(=\left(x^2-2xy+y^2\right)+1\)
\(=\left(x-y\right)^2+1\)
vì \(\left(x-y\right)^2\ge0\Rightarrow\left(x-y\right)^2+1>0\forall x,y\)
vậy ................

x2 > 2( x - 1 )
<=> x2 - 2x + 2 > 0
<=> ( x2 - 2x + 1 ) + 1 > 0
<=> ( x - 1 )2 + 1 > 0 ( luôn đúng ∀ x ∈ R )
Vậy bđt ban đầu được chứng minh

Ta có:
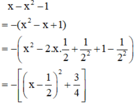
Ta có: 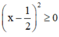 với mọi số thực x
với mọi số thực x
⇒ 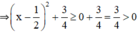 với mọi số thực x
với mọi số thực x
⇒ 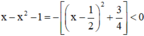 với mọi số thực (ĐPCM)
với mọi số thực (ĐPCM)

a) Ta có: \(x^2-x+1=x^2-2\cdot x\cdot\frac{1}{2}+\frac{1}{4}+\frac{3}{4}=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\)
Ta có: \(\left(x-\frac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\forall x\)
hay \(x^2-x+1>0\forall x\)(đpcm)
b) Ta có: \(-x^2+2x-4=-\left(x^2-2x+4\right)=-\left(x^2-2x+1+3\right)=-\left(x-1\right)^2-3\)
Ta có: \(\left(x-1\right)^2\ge0\forall x\)
\(\Rightarrow-\left(x-1\right)^2\le0\forall x\)
\(\Rightarrow-\left(x-1\right)^2-3\le-3< 0\forall x\)
hay \(-x^2+2x-4< 0\forall x\)(đpcm)

a) \(A=x^2-2x+2=\left(x-1\right)^2+1>0\forall x\inℝ\)
b) \(x-x^2-3=-\left(x^2-x+3\right)\)
\(=-\left(x^2-x+\frac{1}{4}+\frac{11}{4}\right)\)
\(=-\left[\left(x-\frac{1}{2}\right)^2+\frac{11}{4}\right]\)
\(=-\left[\left(x-\frac{1}{2}\right)^2\right]-\frac{11}{4}\le\frac{-11}{4}< 0\forall x\inℝ\)
\(x-x^2-1=-x^2+x-1=-\left(x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}\right)-\dfrac{3}{4}=-\left(x-\dfrac{1}{2}\right)^2-\dfrac{3}{4}\)
Ta có: \(\left(x-\dfrac{1}{2}\right)^2\ge0\forall x\in R\)
\(\Rightarrow-\left(x-\dfrac{1}{2}\right)^2\le0\forall x\in R\)
\(\Rightarrow-\left(x-\dfrac{1}{2}\right)-\dfrac{3}{4}\le-\dfrac{3}{4}< 0\forall x\in R\)
\(\Rightarrow x-x^2-1< 0\forall x\in R\left(đpcm\right)\)
$x-x^2-1$
$=-(x^2-x+1)$
\(=-\left[\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\right]\)
\(=-\left(x-\dfrac{1}{2}\right)^2-\dfrac{3}{4}\le-\dfrac{3}{4}< 0\)
Vậy \(x-x^2-1<0\)\(\forall x\in R\) \(\left(ĐPCM\right)\)