Cho tam giác ABC có đường cao AE có đường cao AE gọi F và D tương ứng là trung điểm các cạnh AB,AC. Gọi G là điểm đối xứng của E qua điểm D. Gọi H là điểm đối xứng của E qua điểm F
A chứng minh rằng AECG là một hình chữ nhật
B chứng minh rằng ba điểm H,A,G thẳng hàng


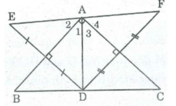
a. Ta có :Vì G đối xứng E qua D nên D là trung điểm EG
Xét tứ giác AGCE có : AC , EG là hai đường chéo
Mà AC cắt EG tại trung điểm mỗi đường
Do đó AGCE là hình bình hành .
Lại có : AE \(\perp\) BC => Góc AEC = 90 độ
Vậy AGCE là hình chữ nhật
b. Ta có : Vì H đối xứng với E qua F nên F là trung điểm HE
Xét tứ giác HAEB có : 2 đường chéo AB , HE
Mà AB cắt HE tại trung điểm mỗi đường
Do đó HAEB là hình bình hành
Lại có : góc AEB = 90 độ
=> HAEB là hình chữ nhật
=> Góc HAE = 90 độ
Mà ta có : AGCE là hình chữ nhật
=> Góc GAE = 90 độ
=> Góc HAE + Góc GAE = 90 độ
Hay góc HAE và góc GAE kề bù
=> H , A , G thẳng hàng
Giúp mình nhớ anh em