Một xe chuyển động thẳng nhanh dần đều qua 2 điểm A,B với các vận tốc vA=3m/s, vB=9m/s. Tính vận tốc tại trung điểm C của AB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1
Tóm tắt: \(v_A=6\left(\dfrac{m}{s}\right);\\ v_B=8\left(\dfrac{m}{s}\right);\\ s_{AC}=s_{CB}\\ v_{tb}=?\)
Giải:
-Vận tốc trung bình là
ADCT: \(v_{tb}=\dfrac{1}{\dfrac{1}{2}\left(\dfrac{1}{v_A}+\dfrac{1}{v_B}\right)}=\dfrac{1}{\dfrac{1}{2}\left(\dfrac{1}{6}+\dfrac{1}{8}\right)}=\dfrac{48}{7}\approx6,86\left(\dfrac{m}{s}\right)\)

Đáp án C
Goị vC là vận tốc của vật tại C. Đặt AB = S
Ta có:
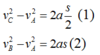
(1) và (2) 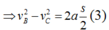
(1) và (3) 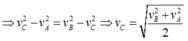

< bài này hơi phức tạp nhưng nếu bạn linh hoạt trong vc sử dụng công thức thì khá oke. Bài này mình áp dụng công thức liên hệ giữa gia tốc, vận tốc và quãng đường >
Đổi: 36 km/h =10 m/s ; 72 km/h =20 m/s
Áp dụng công thức liên hệ giữa gia tốc, vận tốc, quãng đường lên quãng đường AC ta được
\(v_C^2-v_A^2=2s_{AC}a\Rightarrow s_{AC}=\dfrac{v_C^2-v_A^2}{2a}=\dfrac{v_C^2-100}{2a}\) (1)
Áp dụng công thức liên hệ giữa gia tốc, vận tốc, quãng đường lên quãng đường CB ta được
\(v_B^2-v_C^2=2s_{CB}a\Rightarrow s_{CB}=\dfrac{v_B^2-v_C^2}{2a}=\dfrac{400-v_C^2}{2a}\)(2)
Vì C là trung điểm của AB nên \(s_{AC}=s_{BC}\)(3)
Từ (1) , (2) và (3)
\(\Rightarrow\dfrac{v_C^2-100}{2a}=\dfrac{400-v_C^2}{2a}\Rightarrow v_C=5\sqrt{10}\left(\dfrac{m}{s}\right)\approx15,81\left(\dfrac{m}{s}\right)\)
Chọn B
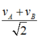

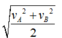
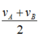
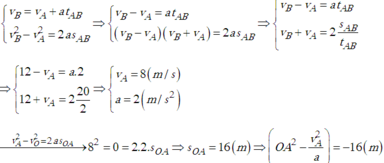
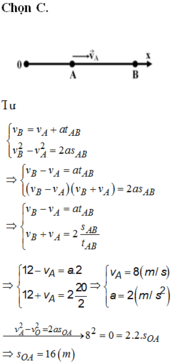
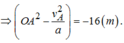
tóm tắt: \(v_A=3\left(\dfrac{m}{s}\right);\\ v_B=9\left(\dfrac{m}{s}\right);\\ s_{AC}=s_{CB}\\ v_{tb}=?\)
Giải:
-Vận tốc trung bình tại điểm C là :
ADCT: \(v_{tb}=\dfrac{1}{\dfrac{1}{2}\left(\dfrac{1}{v_A}+\dfrac{1}{v_B}\right)}=\dfrac{1}{\dfrac{1}{2}\left(\dfrac{1}{3}+\dfrac{1}{9}\right)}=\dfrac{9}{2}=4,5\left(\dfrac{km}{h}\right)\)