Cho a//b , c cắt a tại A , c cắt b tại B . góc A1 và góc B1 là 2 góc so le trong . Chứng minh 2 tia phân giác của 2 góc A1 và góc B1 song song với nhau .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 10 2017
* Góc đồng vị với A 1 ^ bằng 30o, khác A 1 ^ nên b1 không song song với a.
Vậy b1 không trùng với b.
* Góc kề bù với góc đồng vị của A 1 ^ bằng 145o nên góc
đồng vị với A 1 ^ bằng 180o – 145o = 35o = A 1 ^ .
Vậy b2 song song với a nên b2 trùng với b (theo tiên đề Ơ-clit)
KN
3 tháng 7 2019
Ta có: \(\widehat{xAB}=\widehat{ABy'}\)\(\left(xx'//yy',soletrong\right)\)(1)
Mà A1 là phân giác của \(\widehat{xAB}\)nên \(\widehat{xA_1}=\widehat{_1AB}=\frac{\widehat{xAB}}{2}\)(2)
Chứng minh tương tự: \(\widehat{AB_1}=\widehat{_1By'}=\frac{\widehat{ABy'}}{2}\)(3)
Từ (1), (2) và (3) suy ra \(\widehat{_1AB}=\widehat{AB_1}\)
Mà hai góc này ở vị trí so le trong nên \(A_1//B_1\)(đpcm)
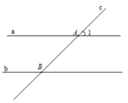
Ta có : tia phân giác góc A1= 1/2 góc A1
tia phân giác góc B1 = 1/2 góc B1
Mà A1=B1(cặp góc so le trong) nên:
Phân giác góc A1 = phân giác góc B1
Ta lại có: Phân giác góc A1 và phân giác góc B1 nằm ở vị trí sole trong
Suy ra: Tia phân giác của 2 góc A1 và B1 song song với nhau