Mem nào giúp bài II kia vs ạ !!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
Đỗ Thanh Hải
CTVVIP
13 tháng 7 2021
1 If my father didn't smoke too much, he wouldn'e have a bad cold
2 If she were tall enough, she could join the basketball team
3 If I had much time, I would visit my grandparents very often
4 If he knew her address, he could visit her
5 If the bike weren't too small, I could ride it
6 If they had enough money, they would buy the tickets for the concerts
7 If I had a car, I wouldn't have to get up early to catch the bus
8 If Mark were't talkative, people would like him
9 If Ken played football well enough, he would be chosen to be in the school team
10 If Emma read book often, her essays wouldn't be bad
7 tháng 1 2022
1,C
2,A
3,C
4,C
5.B
1,A
2,D
3,D
4,A
5,D
1,C
2,B
3,B
4,C
5,C
6,D
7,D
8,D
9,C
10,A
TG
giải giúp mình bài II vs III ạ mình làm rồi nhưng sợ sai (4 điểm)
2
11 tháng 2 2022
Bài II, câu 3 chọn I
4 - high
5 - ride
6 - put it on
7 - happy
9 - looking
10 - not to smoke
Bài III
2 - C
4 - A
TN
1
2 tháng 10 2015
a) Xem hình vẽ.
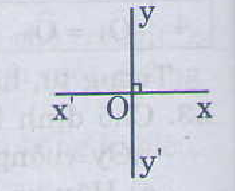
b)
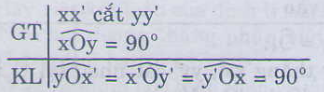
c) Điền vào chỗ trống:
1) (vì là hai góc kề bù).
2) (theo giả thiết và căn cứ vào 1).
3) (căn cứ vào 2).
4) (vì là hai góc đối đỉnh).
5) (căn cứ vào 4 và giả thiết).
6) (vì là hai góc đối đỉnh).
7) (căn cứ vào 6 và 3).
d)Trình bày lại cách chứng minh một cách gọn hơn.
Ta có: (hai góc kề bù) mà
(gt)
nên .
Suy ra
Lại có (hai góc đối đỉnh).
Suy ra .
TA
1
11 tháng 7 2023
2:
a: =(x-y)^2-4
=(x-y-2)(x-y+2)
b: =49-(16x^2-8xy+y^2)
=49-(4x-y)^2
=(7-4x+y)(7+4x-y)
3:
a: =x^2(x^4-x^2+2x+2)
b: =(x+y-x+y)[(x+y)^2+(x-y)(x+y)+(x-y)^2]
=2y(x^2+2xy+y^2+x^2-y^2+x^2-2xy+y^2)
=2y(3x^2+y^2)
YN
11 tháng 7 2023
\(45.\)
\(M=a^3+b^3+3ab\left(a^2+b^2\right)+6a^2b^2\left(a+b\right)\)
\(=\left(a+b\right)\left(a^2-ab+b^2\right)+3ab\left[\left(a^2+2ab+b^2\right)-2ab\right]+6a^2b^2\left(a+b\right)\)
\(=\left(a+b\right)\left(a^2-ab+b^2\right)+3ab\left[\left(a+b\right)^2-2ab\right]+6a^2b^2\left(a+b\right)\)
\(=a^2-ab+b^2+3ab\left(1-2ab\right)+6a^2b^2\)
\(=a^2-ab+b^2+3ab-6a^2b^2+6a^2b^2\)
\(=a^2+2ab+b^2\)
\(=\left(a+b\right)^2\)
\(=1^2\)
\(=1\).
11 tháng 7 2023
42:
a^3+b^3+c^3-3abc
=(a+b)^3+c^3-3ab(a+b)-3bac
=(a+b+c)(a^2+2ab+b^2-ac-bc+c^2)-3ab(a+b+c)
=0
=>a^3+b^3+c^3=3abc
44:
a: x^3+y^3+3xy
=(x+y)^3-3xy(x+y)+3xy
=1^3-3xy+3xy=1
b: x^3-y^3-3xy
=(x-y)^3+3xy(x-y)-3xy
=1^3+3xy-3xy=1
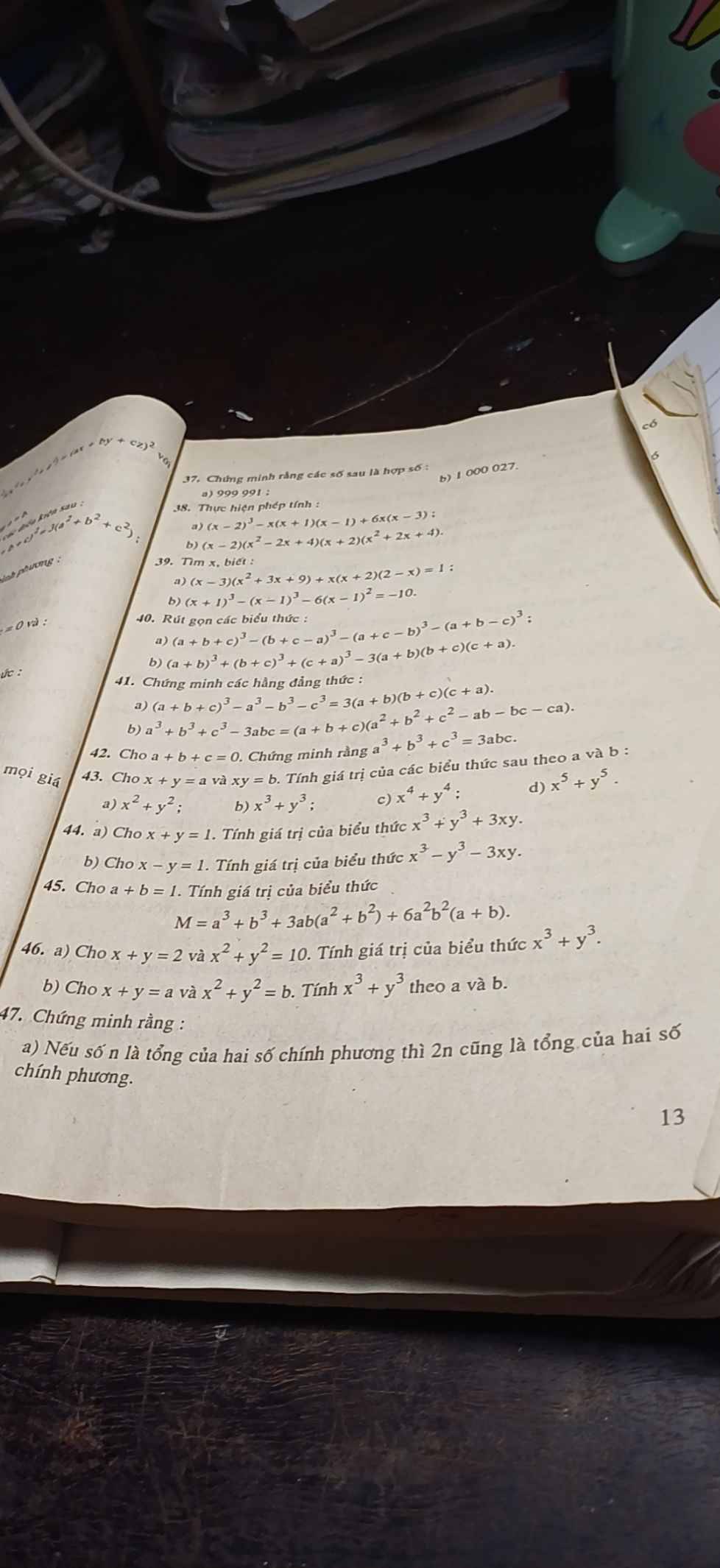
bài nào v bn?