Ai chỉ rm mấy câu này với .
Em cảm ơn nhiều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1. If you are calm, you won't make a wrong decision.
2. These wonderful poems were written by a great poet.
3.Because of rained heavily, Jane didn't go fishing yesterday.
4.Vietnamese people use Khue Van pavilion as a symbol of Hanoi.
5. His idea is not the same as me.
6. Those modern paintings are not as expensive as these Dong Ho paintings.
7. What food do you like?
8.These machines are used by chefs to mix the ingredients.
9. It i've most seen such a boring movie.
10. There are not many eggs in the fridge.
11.They started living there 2 years ago.
12. I have never drunk cocktail before.
13.This exercise is not as difficult as the last one.
14. I find playing computer games boring.
15. The new building has the same height as the old one.
16. She didn't have enough eggs to make an omelette.
17. In spite of promising that wouldn't be late, he didn't arrive until 9 o'clock.
18. I didn't use to listen to Western music some years ago.
19. My mum used to be a chef in Cham restaurant, but now she is tired.

Chắc đề đúng là \(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...\)
- Với \(n=1\) đẳng thức đúng
- Giả sử đẳng thức cũng đúng với \(n=k>1\) hay:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}=\dfrac{k^2}{4k^2+1}\)
- Ta cần chứng minh nó cũng đúng với \(n=k+1\) hay:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\)
Thật vậy, ta có:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{4+\left(2k+1\right)^4}\)
\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(2k+1\right)^4+4\left(2k+1\right)^2+4-4\left(2k+1\right)^2}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+4k+3\right)^2-\left(4k+2\right)^2}\)
\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{k^2\left(4k^2+8k+5\right)+2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}\)
\(=\dfrac{\left(k+1\right)^2\left(4k^2+1\right)}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{\left(k+1\right)^2}{4k^2+8k+5}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\) (đpcm)

a, thay x=25 vào A ta có:
\(A=\dfrac{\sqrt{x}}{\sqrt{x}-1}=\dfrac{\sqrt{25}}{\sqrt{25}-1}=\dfrac{5}{5-1}=\dfrac{5}{4}\)
b, \(P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{x\sqrt{x}-1}-\dfrac{2}{\sqrt{x}-1}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{\sqrt{x^3}-1}-\dfrac{2\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{2x+2\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}.\dfrac{3x+3-2x-2\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}\left(x-2\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)^2\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)

\(=2\sqrt{3}-10\sqrt{3}-\sqrt{3}+\dfrac{5\sqrt{3}}{2}=\dfrac{5\sqrt{3}}{2}-9\sqrt{3}=\dfrac{5\sqrt{3}-18\sqrt{3}}{2}=\dfrac{-13\sqrt{3}}{2}\)
\(=\dfrac{1}{2}.4\sqrt{3}-2.5\sqrt{3}-\sqrt{3}+5.\dfrac{\sqrt{3}}{2}\)
\(=2\sqrt{3}-10\sqrt{3}-\sqrt{3}+\dfrac{5\sqrt{3}}{2}\)
\(=-9\sqrt{3}+\dfrac{5\sqrt{3}}{2}=\dfrac{-18\sqrt{3}+5\sqrt{3}}{2}=-\dfrac{13\sqrt{3}}{2}\)

Giải hpt:
Đặt: \(\left[{}\begin{matrix}\sqrt{x-1}=a\\y+1=b\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}3a-2b=-1\\5a-9b=-13\end{matrix}\right.< =>\left\{{}\begin{matrix}15a-10b=-5\\15a-27b=-39\end{matrix}\right.< =>\left\{{}\begin{matrix}b=2\\15a-27\cdot2=-39\end{matrix}\right.< =>\left\{{}\begin{matrix}b=2\\a=1\end{matrix}\right.\)
Thay: \(\left[{}\begin{matrix}\sqrt{x-1}=1\\y+1=2\end{matrix}\right.< =>\left[{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)

\(A=\sqrt{2a\left(b+1\right)}+\sqrt{2b\left(c+1\right)}+\sqrt{2c\left(a+1\right)}\)
\(A=\dfrac{1}{\sqrt{2}}\sqrt{4a\left(b+1\right)}+\dfrac{1}{\sqrt{2}}\sqrt{4b\left(c+1\right)}+\dfrac{1}{\sqrt{2}}\sqrt{4c\left(a+1\right)}\)
\(A\le\dfrac{1}{2\sqrt{2}}\left(4a+b+1\right)+\dfrac{1}{2\sqrt{2}}\left(4b+c+1\right)+\dfrac{1}{2\sqrt{2}}\left(4c+a+1\right)\)
\(A\le\dfrac{1}{2\sqrt{2}}\left[5\left(a+b+c\right)+3\right]=2\sqrt{2}\)
\(A_{max}=2\sqrt{2}\) khi \(a=b=c=\dfrac{1}{3}\)


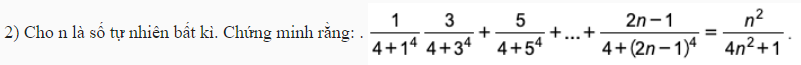






17. Despite promising that he wouldn't be late, he didn't arrive until 9 o'clock.
18. I didn't use to listen to Western music some years ago.
19. My mum used to be a chef in Cham restaurant, but now he is retired.
20. There used to be a market here in 2003.
21. The new restaurant looks good. However, it seems to have few customers.
22. They didn't use to know how to drive a car, but now they can drive well.
23. We planned to visit Petronas in the afternoon. However, we couldn't afford the fee.
24. Despite being sick, Marry didn't leave the meeting until it ended.
25. There used to be less vehicles on the roads in the past.