Tại sao gọi hình chiếu trục đo có phép chiếu song song
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 12 2021
Hình chiếu trục đo: Là hình biểu diễn ba chiều của vật thể được xây dựng trên cơ sở phép chiếu song song.
=> Chọn A
19 tháng 7 2018
Vì hệ số biến dạng p = r = 1. Mà p và r lần lượt là hệ số biến dạng trên trục O’X’ và O’Z’ nên các mặt của vật thể song song với mặt phẳng tọa độ XOZ không bị biến dạng.
22 tháng 9 2023
Tham khảo:
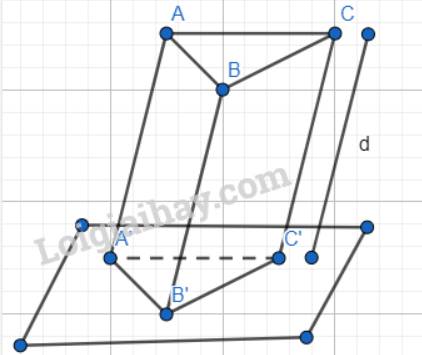
Nếu tam giác A′B′C′ là hình chiếu của tam giác ABC theo phương d thì tam giác ABC là hình chiếu của tam giác A′B′C′ vì tam giác ABC là tập hợp tất cả các hình chiếu của các điểm thuộc A'B'C' qua phép chiếu song song theo phương d.
CM
26 tháng 11 2018
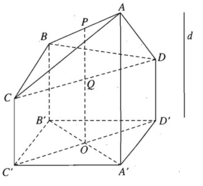
Cho tứ diện ABCD. Gọi d là một đường thẳng không song song với với các cạnh của tứ diện và (α) là một mặt phảng cắt d. Gọi A’, B’, C’, D’ lần lượt là hình chiếu của A, B, C, D trên mặt phẳng (α). Gọi P và Q lần lượt là trung điểm của hai cạnh đối diện AB và CD. Khi đó hình chiếu của P’ và Q’ của P và Q sẽ lần lượt là trung điểm của A’B’ và C’D’.
Muốn cho A’, B’, C’, D’ là các đỉnh của một hình bình hành ta chỉ cần chọn phương chiếu d sao cho d song song với đường thẳng PQ.
Vậy để hình chiếu song song của một tứ diện là một hình bình hành ta có thể chọn :
- Phương chiếu d là phương của một trong ba đường thẳng đi qua trung điểm của hai cạnh đối diện của tứ diện cho trước.
- Mặt phẳng chiếu (α) là mặt phẳng tùy ý, nhưng phải cắt đường thẳng d.
Vì tất cả các đường vẽ theo cũng chiều(cùng góc) là song song (Gần như thôi nhé)
vd hình dưới 2 đường mũi tên chỉ là // với nhau nek