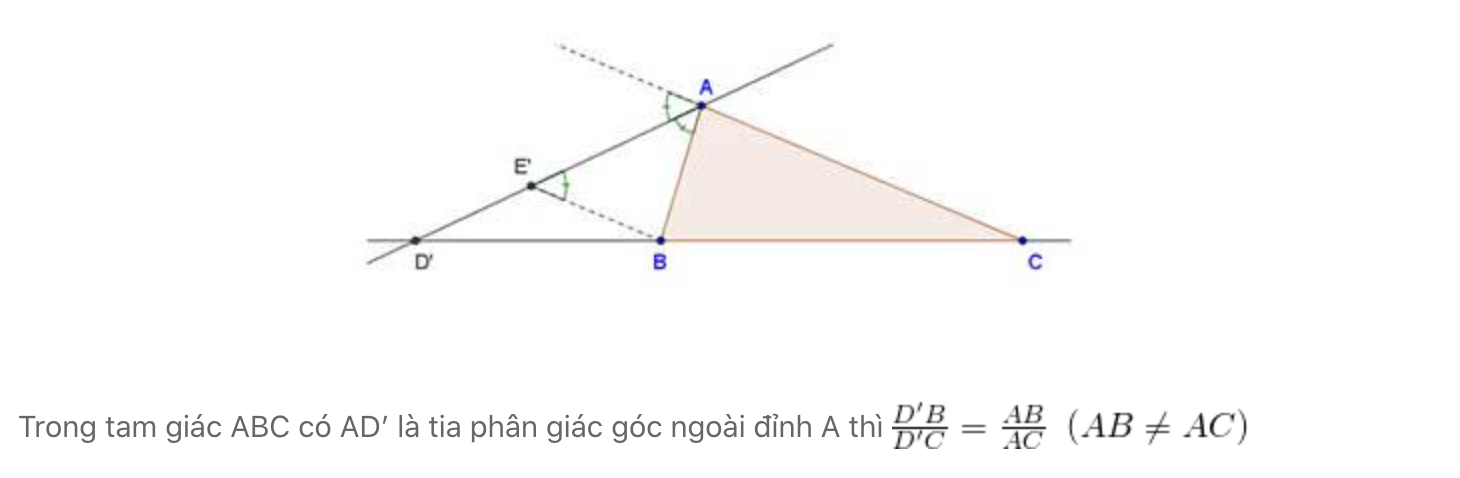
Chứng minh rằng tia đi qua đỉnh một góc của một tam giác và chia cạnh đối diện thành hai đoạn thẳng tương ứng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy là tia phân giác của góc đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 1 2022
Câu 9: Khẳng định nào sau đây
A . Hai góc bằng nhau là hai góc đối đỉnh.
B. Đường trung trực của đoạn thẳng thì đi qua trung điểm của đoạn thẳng ấy.
C. Hai đường thẳng không cắt nhau thì song song.
D. Đường trung trực của một đoạn thẳng là đường vuông góc với đoạn thẳng đó.
.Câu 10: Trong các phát biểu sau đây thì phát biểu nào đúng?
A. Hai tia phân giác của cặp góc bù nhau thì vuông góc với nhau.
B. Hai tia phân giác của cặp góc kề nhau thì vuông góc với nhau.
C. Hai tia phân giác của cặp góc đối đỉnh thì vuông góc với nhau.
D. Hai tia phân giác của cặp góc kề bù thì vuông góc với nhau.
5 tháng 1 2021
https://diendan.hocmai.vn/threads/chung-minh-dinh-li-talet.287639/
CM
13 tháng 4 2017
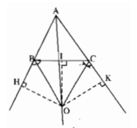
Giả sử hai tia phân giác của các góc ngoài tại đỉnh B và C của tam giác ABC cắt nhau tại O. Ta sẽ chứng minh AO là tia phân giác của góc A.
Kẻ các đường vuông góc OH, OI, OK từ O lần lượt đến các đường thẳng AB, BC, AC.
Vì BO là tia phân giác của góc HBC nên OH = OI (1)
Vì CO là tia phân giác của góc KCB nên OI = OK (2)
Từ (1) và (2) suy ra OI = OH = OK
(3)
Suy ra: O thuộc đường phân giác của góc BAC.
Suy ra AO là tia phân giác của góc BAC và ta có điều phải chứng minh.
29 tháng 8 2015
Dễ ẹt;
Giả sử \(\Delta\)ABC vuông tại A có phân giác AD sao cho DC=3BD;đương cao AH
Từ B kẻ đường thẳng song song với AC cắt AD tại I => BI vuông góc AB
Vì AD là p/g góc A => góc BAD=45 nên tam giác BAI vuông cân tại B nên BA=BI
Vì BI // AC nên \(\left(\frac{BI}{AC}\right)=\left(\frac{BD}{DC}\right)=\left(\frac{BD}{3BD}\right)=\frac{1}{3}\) (định lí Ta lét)
mà BI=AB nên \(\frac{AB}{AC}=\frac{1}{3}\)
Cm \(\Delta\)AHC đồng dạng \(\Delta\)BHA(g.g) nên \(\frac{BH}{HA}=\frac{HA}{HC}=\frac{AB}{AC}=\frac{1}{3}\)
nên \(BH=\frac{1}{3}AH\);\(HC=3AH\)nên \(\frac{BH}{HC}=\frac{1}{9}\)
6 tháng 9
Giả sử
Δ
ΔABC vuông tại A có phân giác AD sao cho DC=3BD;đương cao AH
Từ B kẻ đường thẳng song song với AC cắt AD tại I => BI vuông góc AB
Vì AD là p/g góc A => góc BAD=45 nên tam giác BAI vuông cân tại B nên BA=BI
Vì BI // AC nên
(
B
I
A
C
)
=
(
B
D
D
C
)
=
(
B
D
3
B
D
)
=
1
3
(
AC
BI
)=(
DC
BD
)=(
3BD
BD
)=
3
1
(định lí Ta lét)
mà BI=AB nên
A
B
A
C
=
1
3
AC
AB
=
3
1
Cm
Δ
ΔAHC đồng dạng
Δ
ΔBHA(g.g) nên
B
H
H
A
=
H
A
H
C
=
A
B
A
C
=
1
3
HA
BH
=
HC
HA
=
AC
AB
=
3
1
nên
B
H
=
1
3
A
H
BH=
3
1
AH;
H
C
=
3
A
H
HC=3AHnên
B
H
H
C
=
1
9
HC
BH
=
9
1