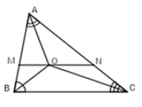
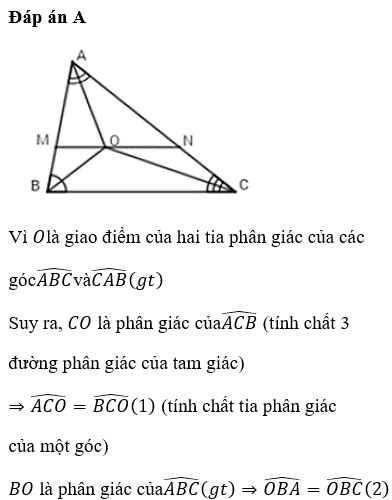
Cho tam giác ABC. Tia phân giác của góc B , góc C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC cắt AB tại M và AC tại N.Chứng minh rằng MN = BM + CN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TA
31 tháng 8 2020
Ta có: BI là phân giác \(\widehat{ABC}\Rightarrow\widehat{B_1}=\widehat{B_2}\)
CI là phân giác \(\widehat{ACB}\Rightarrow\widehat{C_1}=\widehat{C_2}\)
\(MN//BC\Rightarrow\widehat{I_1}=\widehat{B_2}\),\(\widehat{I_2}=\widehat{C_2}\)
+) Vì \(\widehat{B_1}=\widehat{B_2}\);\(\widehat{I_1}=\widehat{B_2}\)
\(\Rightarrow\widehat{B_1}=\widehat{I_1}\Rightarrow\Delta MBI\)cân tại M
\(\Rightarrow MB=MI\)
+) Vì \(\widehat{C_1}=\widehat{C_2}\);\(\widehat{I_1}=\widehat{C_2}\)
\(\Rightarrow\widehat{C_1}=\widehat{I_2}\Rightarrow\Delta NCI\)Cân tại N
\(\Rightarrow NC=NI\)
Ta có: \(MN=MI+NI\)
mà \(MB=MI\);\(NC=NI\)
\(\Rightarrow MN=MB+NC\left(đpcm\right)\)
3 tháng 3 2020
Bài làm
Ta có: MN // BC
=> ^MIB = ^IBC ( so le trong )
Mà ^MBI = ^IBC ( BI phân giác )
=> ^MIB = ^ MBI
=> Tam giác MBI cân tại M
=> MB = MI
Lại có: MN // BC
=> ^NIC = ^ICB ( so le trong )
Mà ^ICN = ^ICB ( Do CI phân giác )
=> ^NIC = ^ICN
=> Tam giác INC cân tại N
=> IN = NC
Ta có: MN = MI + IN
Hay MN = MB + NC
Vậy MN = MB + NC ( đpcm )
Bạn có kết quả bài này chưa giải giúp mk với
bài lớp mấy