cho a,b,c,d,e dương CMR \(\dfrac{a}{b+c}+\dfrac{b}{c+d}+\dfrac{c}{d+e}+\dfrac{d}{e+a}+\dfrac{e}{a+b}\ge\dfrac{5}{2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HN
26 tháng 10 2017
Đặt \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{d}{e}=\dfrac{e}{f}=\dfrac{a+b+c+d+e}{b+c+d+e+f}=k\)
Ta có:
\(\dfrac{a}{f}=\dfrac{a}{b}.\dfrac{b}{c}.\dfrac{c}{d}.\dfrac{d}{e}.\dfrac{e}{f}=k^5=\left(\dfrac{a+b+c+d+e}{b+c+d+e+f}\right)^5\)
27 tháng 10 2017
Đúng là góc học tập của cậu tràn trề đại số và rất ít hình học. 
14 tháng 12 2021
Đặt \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{d}{e}=k\Rightarrow a=bk;b=ck;c=dk;d=ek\)
\(\Rightarrow a=bk=ck^2=dk^3=ek^4;b=ek^3\)
\(\Rightarrow\dfrac{a}{e}=\dfrac{ek^4}{e}=k^4\left(1\right)\)
Ta có \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{d}{e}\Rightarrow\dfrac{a^4}{b^4}=\dfrac{b^4}{c^4}=\dfrac{c^4}{d^4}=\dfrac{d^4}{e^4}=\dfrac{2a^4+3b^4+4c^4+5d^4}{2b^4+3c^4+4d^4+5e^4}\left(2\right)\)
Lại có \(\dfrac{a^4}{b^4}=\left(\dfrac{a}{b}\right)^4=\left(\dfrac{ek^4}{ek^3}\right)^4=k^4\left(3\right)\)
\(\left(1\right)\left(2\right)\left(3\right)\RightarrowĐpcm\)
19 tháng 2 2021
a) Ta có: \(\dfrac{a}{b}=\dfrac{c}{d}\)
\(\Leftrightarrow\dfrac{b}{a}=\dfrac{d}{c}\)
\(\Leftrightarrow\dfrac{b}{a}-1=\dfrac{d}{c}-1\)
\(\Leftrightarrow\dfrac{b-a}{a}=\dfrac{d-c}{c}\)
\(\Leftrightarrow\dfrac{a-b}{a}=\dfrac{c-d}{c}\)
\(\Leftrightarrow\dfrac{a}{a-b}=\dfrac{c}{c-d}\)(đpcm)
thì nó khó thiệt mà
23 tháng 4 2017
Áp dụng BĐT Cauchy-Schwarz dạng Engel ta có:
\(VT=\dfrac{a^2}{a+b}+\dfrac{b^2}{b+c}+\dfrac{c^2}{c+d}+\dfrac{d^2}{a+d}\)
\(\ge\dfrac{\left(a+b+c+d\right)^2}{a+b+b+c+c+d+d+a}\)
\(=\dfrac{\left(a+b+c+d\right)^2}{2\left(a+b+c+d\right)}=\dfrac{a+b+c+d}{2}=\dfrac{1}{2}=VP\)
Đẳng thức xảy ra khi \(a=b=c=d=\dfrac{1}{4}\)
13 tháng 6 2017
Đặt \(k=\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{d}{e}\)
Ta có: \(k=\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{d}{e}=\dfrac{a+b+c+d}{b+c+d+e}\) ( t/c dãy tỉ số bằng nhau )
\(\Rightarrow k^4=\left(\dfrac{a+b+c+d}{b+c+d+e}\right)^4\) (1)
\(k^4=\dfrac{a}{b}.\dfrac{b}{c}.\dfrac{c}{d}.\dfrac{d}{e}=\dfrac{a}{e}\) (2)
Từ (1), (2) \(\Rightarrow\left(\dfrac{a+b+c+d}{b+c+d+e}\right)^4=\dfrac{a}{e}\left(đpcm\right)\)
Vậy...
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 7 2021
Đặt vế trái BĐT là P
Ta có:
\(\left(\dfrac{a^3}{b+c}+\dfrac{b^3}{c+a}+\dfrac{c^3}{a+b}\right)\left(a\left(b+c\right)+b\left(c+a\right)+c\left(a+b\right)\right)\ge\left(a^2+b^2+c^2\right)^2\)
\(\Rightarrow P.\left(2ab+2bc+2ca\right)\ge1\)
\(\Rightarrow P\ge\dfrac{1}{2\left(ab+bc+ca\right)}\ge\dfrac{1}{2\left(a^2+b^2+c^2\right)}=\dfrac{1}{2}\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{\sqrt{3}}\)
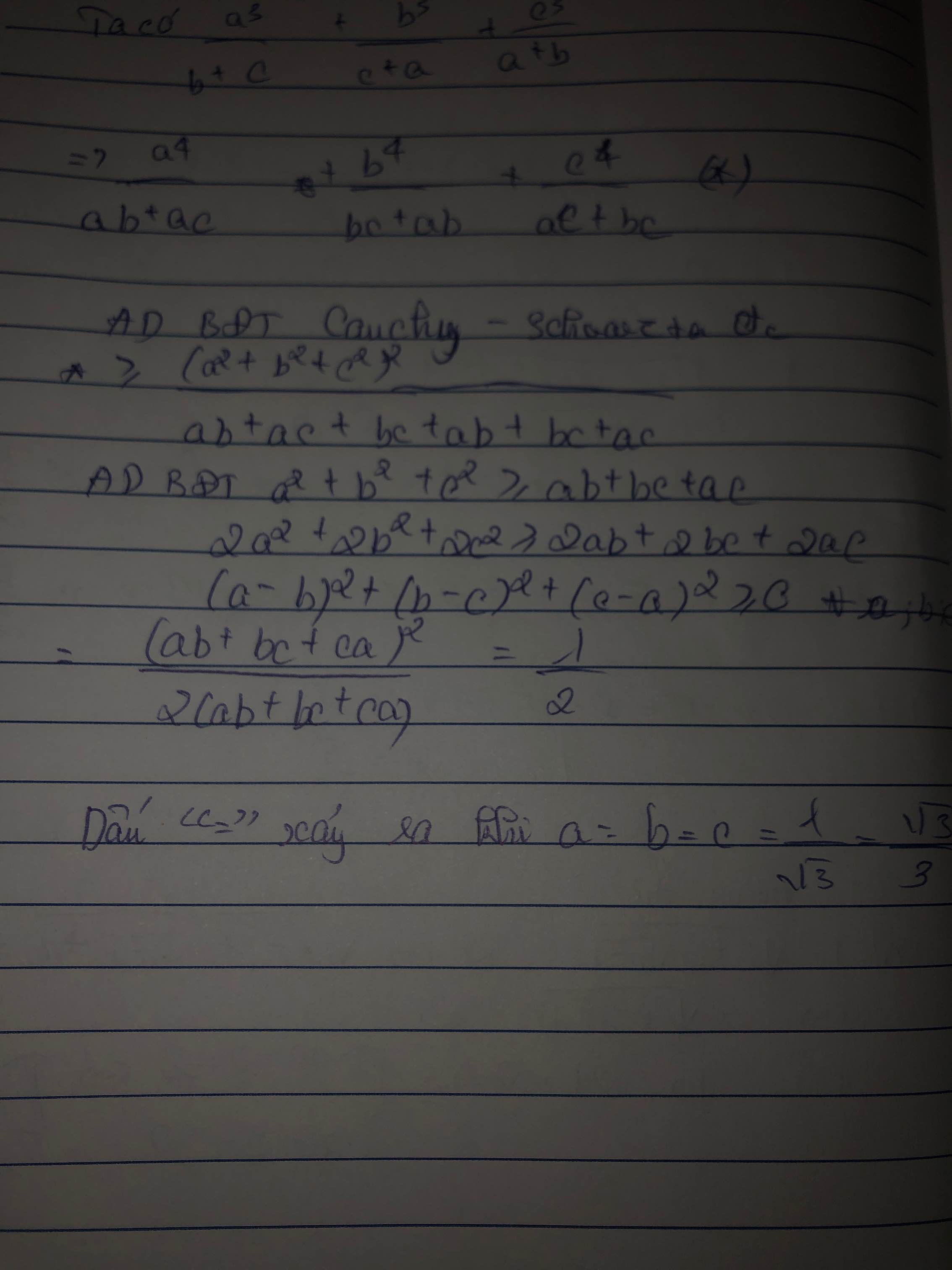
Áp dụng cauchy-schwarz:
\(\dfrac{a}{b+c}+\dfrac{b}{c+d}+\dfrac{c}{d+e}+\dfrac{d}{e+a}+\dfrac{e}{a+b}=\dfrac{a^2}{ab+ac}+\dfrac{b^2}{bc+bd}+\dfrac{c^2}{cd+ce}+\dfrac{d^2}{ed+ad}+\dfrac{e^2}{ae+be}\ge\dfrac{\left(a+b+c+d\right)^2}{ab+ac+ad+ae+bc+bd+be+cd+ce+de}\)
Giờ chỉ cần chứng minh
\(ab+ac+ad+ae+bc+bd+be+cd+ce+de\le\dfrac{2}{5}\left(a+b+c+d+e\right)^2\)
\(\Leftrightarrow ab+ac+ad+ae+bc+bd+be+cd+ce+de\le2\left(a^2+b^2+c^2+d^2+e^2\right)\)
điều này hiển nhiên đúng theo AM-GM:
\(ab\le\dfrac{a^2+b^2}{2};ac\le\dfrac{a^2+c^2}{2};ad\le\dfrac{a^2+d^2}{2}...\)
Cứ vậy ta thu được đpcm .Dấu = xảy ra khi a=b=c=d=e
P/s: : ]