Có 64 tờ giấy bạc gồm 3 loại 2000đ, 5000đ, và 10000d. Biết rằng tổng giá trị mỗi loại giấy bạc trên đều bằng nhau. Hỏi mỗi loại giấy bạc có bao nhiêu tờ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số tờ giấy bạc mỗi loại lần lượt là a,b,c (a,b,c thuộc N* )
Có số tờ giấy bạc mỗi loại và mệnh giá mỗi loại là 2 đại lượng tỉ lệ nghịch, mà giá trị của các loại tiền bằng nhau nên ta có: 2000a=5000b=20000c và a+b+c=75 =>2000a/20000=5000b/20000=20000c/20000 => a/10=b/40=c/1
Áp dụng tính chất dãy tỉ số bằng nhau có: a/10=b/40=c/1=a+b+b/10+40+1=75/51=25/17
=> a/10=25/17, b/40=25/17, c/1=25/17 => a=25/17.10, b=25/17.40, c=25/17.1 (bạn tự tính rồi kết luận nhé)
Gọi giá tiền 3 loại đều bằng nhau là a ( a thuộc N sao ) ; x,y,z lần lượt là số tờ của 2000đ;5000đ;2000đ
Có : x+y+z = 75
Lại có : a = 2000.x=5000.y=20000.z
=> x = 10z ; y = 4z
Thay x=10z và y=4z thì :
10z+4z+z = 75
=> 15z = 75
=> z = 5 => x = 50 ; y = 20

Gọi số tờ tiền loại 2000 đồng là a ; loại 5000 đồng là b ; loại 10000 đồng là c (a;b;c > 0)
Ta có a + b + c = 64
Lại có 2000a = 5000b = 10000c
=> 2a = 5b = 10c
=> \(\frac{2a}{10}=\frac{5b}{10}=\frac{10c}{10}\)
=> \(\frac{a}{5}=\frac{b}{2}=\frac{c}{1}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\frac{a}{5}=\frac{b}{2}=\frac{c}{1}=\frac{a+b+c}{5+2+1}=\frac{64}{8}=8\)
=> \(\hept{\begin{cases}a=40\\b=16\\c=8\end{cases}}\)
Vậy số tờ tiền loại 2000 đồng là 40 tờ ; loại 5000 đồng là 16 tờ ; loại 10000 đồng là 8 tờ

Có : 50 tờ 2000 đồng ; 20 tờ 5000 đồng và 5 tờ 20000 đồng
k mk nha

Gọi x , y , z là tờ giấy bạc theo thứ tự là loại : 20000 đồng , 50000 đồng , 100000 đồng
Ta có x + y + z = 16 ; 20000x = 50000y = 100000z
=>\(\frac{x}{5}=\frac{y}{2}=\frac{z}{1}\)
Theo tính chất bằng nhau của tỉ số
+> \(\frac{x+y+z}{5+2+1}=\frac{16}{8}=2\)
Vậy sau khi tính ta đc lần lượt các loại tiền có số tờ là 10 ; 4 ; 2

Gọi số tờ giấy bạc 20000,50000,100000 lần lượt là x,y,z (x,y,z \(\in N\))
Vì tổng gtrị của mỗi tờ giấy bạc đều bằng nhau
=> 20000x = 50000y = 100000z
Hay 2x = 5y = 10z => \(\frac{x}{5}=\frac{y}{2}=\frac{z}{1}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{5}=\frac{y}{2}=\frac{z}{1}=\frac{x+y+z}{5+2+1}=\frac{64}{8}=8\)
\(\frac{x}{5}=8\Rightarrow x=40\)
\(\frac{y}{2}=8\Rightarrow y=16\)
\(\frac{z}{1}=8\Rightarrow z=8\)
Vậy có 40 tờ giấy bạc 20000đ
16 tờ giấy bạc 50000đ
8 tờ giấy bạc 100000đ
Gọi số tờ giấy bạc loại 2000 đồng, 5000 đồng, 10 000 đồng theo thứ tự là x, y, z (x,y,z∈N∗). Theo bài ra ta có:
2000x=5000y=10000z và x+y+z=64
Từ 2000x=5000y⇒x5=y7.
Từ 5000y=10000z⇒y2=z1.
Do đó: x5=y2=z1=x+y+z5+2+1=648=8x5=y2=z1=x+y+z5+2+1=648=8
Vậy có 40 tờ giấy bạc loại 2000 đồng, 16 tờ loại 5000 đồng và 8 tờ 10 000 đồng.

Đề phải là 10000 mới đúng
Gọi số tờ giấy bạc 2000 đồng là x, số tờ giấy bạc 5000 đồng là y, số tờ giấy bạc 10000 đồng là z (x,y,z thuộc N; khác 0; đơn vị là đồng)
=>x.2000 = y.5000 = z.10000
=>\(\frac{x.2000}{1000}=\frac{y.5000}{1000}=\frac{z.10000}{1000}\)
=>x.2 = y.5 = z.10
=>\(\frac{x}{5}=\frac{y}{2};\frac{y}{10}=\frac{z}{5}\)
Ta có:
\(\frac{x}{5}=\frac{y}{2}=>\frac{x}{25}=\frac{y}{10}\)
\(\frac{y}{10}=\frac{z}{5}=>\frac{y}{10}=\frac{z}{5}\)
=>\(\frac{x}{25}=\frac{y}{10}=\frac{z}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{25}=\frac{y}{10}=\frac{z}{5}\) =\(\frac{x+y+z}{25+10+5}\) =\(\frac{64}{40}\) =\(\frac{8}{5}\)
=>\(\hept{\begin{cases}\frac{x}{25}=\frac{8}{5}\\\frac{y}{10}=\frac{8}{5}\\\frac{z}{5}=\frac{8}{5}\end{cases}}\) =>\(\hept{\begin{cases}x=\frac{8}{5}.25\\y=\frac{8}{5}.10\\z=\frac{8}{5}.5\end{cases}}\) =>\(\hept{\begin{cases}x=40\\y=16\\z=8\end{cases}}\) Vậy\(\hept{\begin{cases}x=40\\y=16\\z=8\end{cases}}\)
Vậy có 40 tờ giấy bạc loại 2000 đồng, 16 tờ giấy bạc loại 5000 đồng và 8 tờ giấy bạc loại 10000 đồng
10 000 chứ có đâu 16 000 bạn?
Gọi x,y,z là số tờ tiền các loại 2000,5000,10000
Khi đó:
2000x=5000y=10000z
=> 2x=5y=10z
=> x/5=y/2=z
Mà x+y+z=64
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
x/5+y/2+x/1=x+y+z/5+2+1=64/8=8
=> x=40
y=16
z=8
Đ/S:...

Gọi x, y, z lần lượt là số tờ giấy bạc các loại 2000đ, 5000đ, và 10000đ (x; y; z ∈ N* và x; y; z < 16).
Có tất cả 16 tờ giấy bạc nên ta có: x + y + z = 16
2000.x = 5000.y = 10000.z
Suy ra: 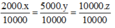
Hay 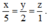
Theo tính chất dãy tỉ số bằng nhau ta có:
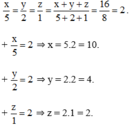
Vậy có 10 ờ loại 2000đ, 4 tờ loại 5000đ và 2 tờ loại 10000đ
Gọi số tờ tiền loại 2000đ là a, 5000đ là b, 10000đ là c => a + b + c =16
Ta có: a.2000 = b.5000 = c.10000
\(\Rightarrow a:\dfrac{1}{2000}=b:\dfrac{1}{5000}=c:\dfrac{1}{10000}\)
\(\Rightarrow\dfrac{a}{\dfrac{1}{2000}}=\dfrac{b}{\dfrac{1}{5000}}=\dfrac{c}{\dfrac{1}{10000}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{\dfrac{1}{2000}}=\dfrac{b}{\dfrac{1}{5000}}=\dfrac{c}{\dfrac{1}{10000}}=\dfrac{a+b+c}{\dfrac{1}{2000}+\dfrac{1}{5000}+\dfrac{1}{10000}}=\dfrac{16}{\dfrac{1}{1250}}=20000\)
\(\Rightarrow\dfrac{a}{\dfrac{1}{2000}}=20000\Rightarrow a=20000.\dfrac{1}{2000}=10\)
\(\dfrac{b}{\dfrac{1}{5000}}=20000\Rightarrow b=20000.\dfrac{1}{5000}=4\)
\(\dfrac{c}{\dfrac{1}{10000}}=20000\Rightarrow c=20000.\dfrac{1}{10000}=2\)
Vậy ...
Tham khảo trên Google nhé,ngại chép lại,Trên Google khác số nên tự hiểu rồi chỉnh sửa nhé!