Bài 6: Cho hai đường tròn (O; R) và (O’; r) tiếp xúc ngoài tại A. Vẽ hai tia gốc A và vuông
góc với nhau, chúng cắt các đường tròn (O; R) và (O’; r) lần lượt tại B và C.
Xác định vị trí của các tia đó để ABC có diện tích lớn nhất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

1 tháng 1 2022
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
TỪ (1) và (2) suy ra OM⊥AB

30 tháng 12 2021
a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA⊥BC

14 tháng 5 2023
a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét ΔABE và ΔADB có
góc ABE=góc ADB
góc BAE chung
=>ΔABE đồng dạng với ΔADB
=>AB^2=AE*AD



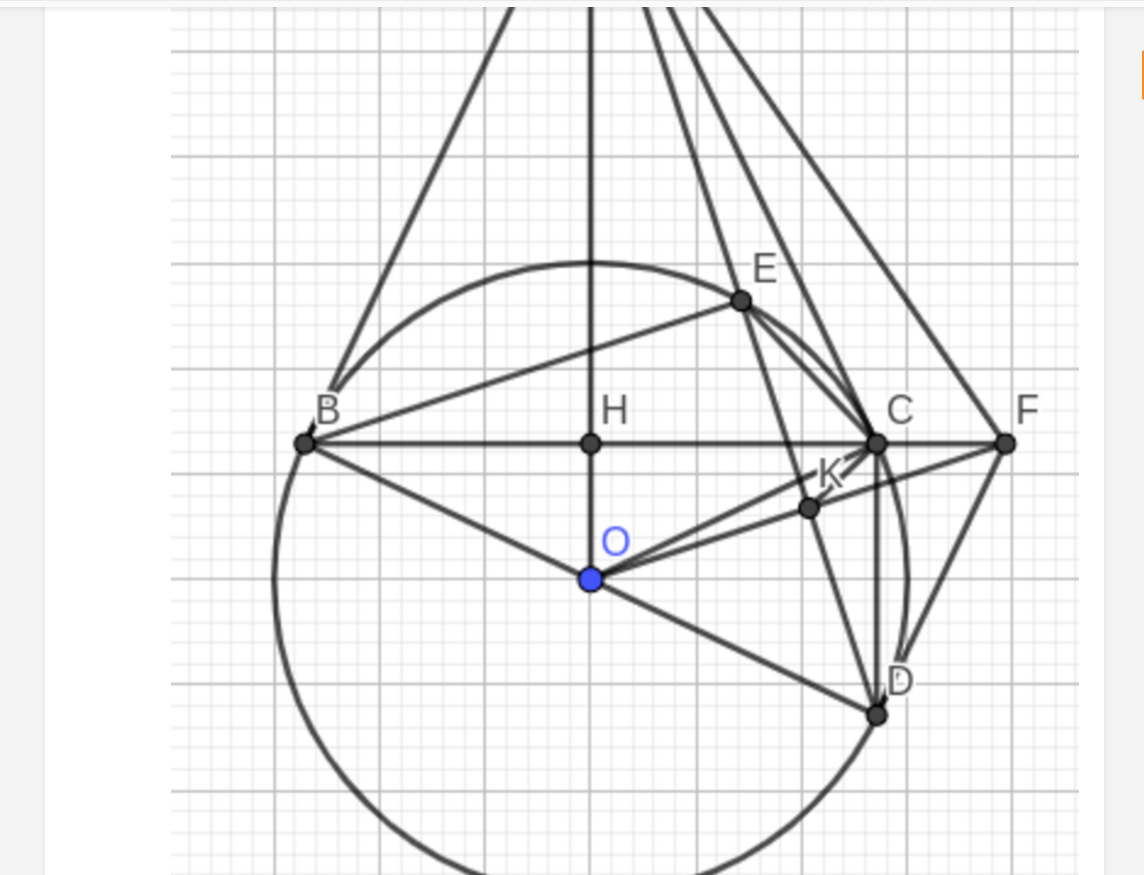
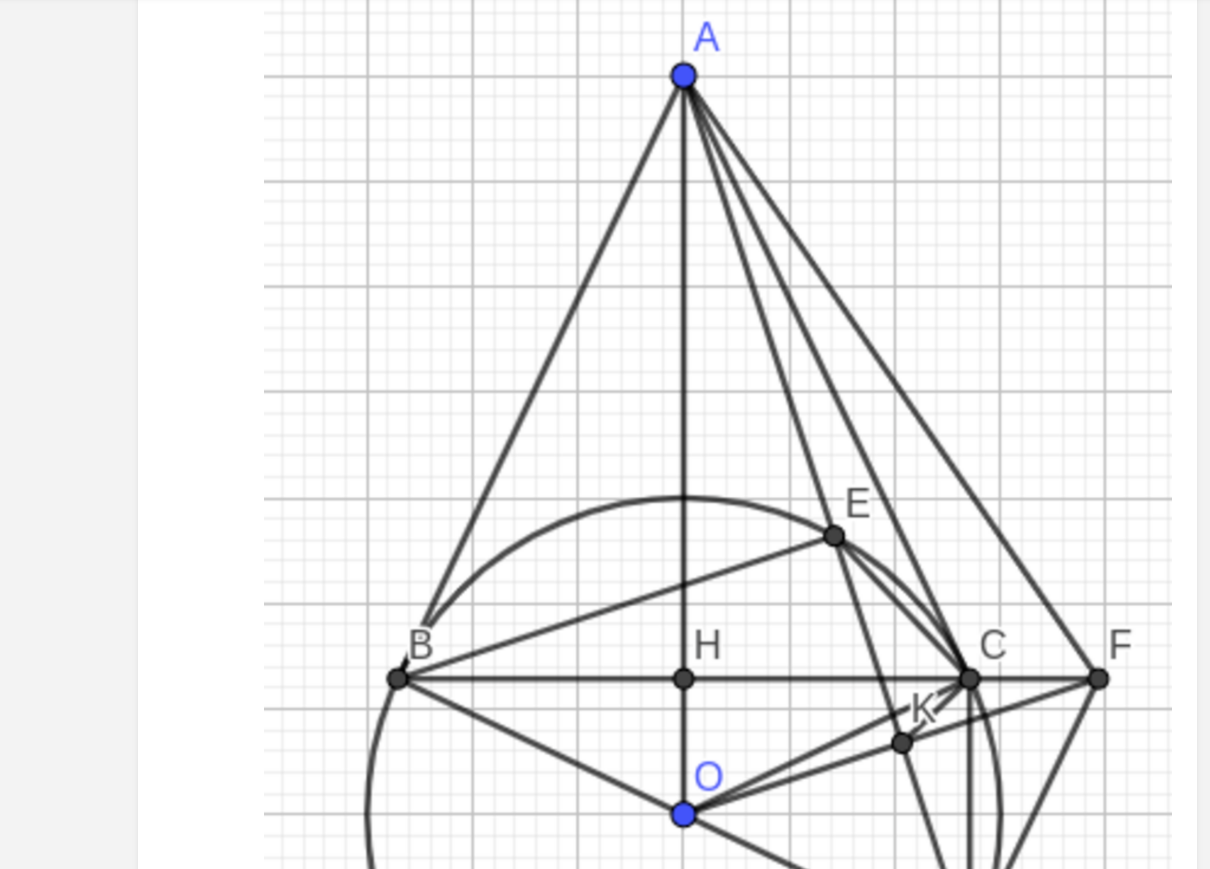
ta có :
\(\widehat{OAB}+\widehat{O'AC}=90^o\Rightarrow\hept{\begin{cases}AC=2AO\cos\widehat{OAC}\\AB=2AO'\cos\widehat{O'AB}=2AO'\sin\widehat{OAC}\end{cases}}\)
ta có : \(S_{ABC}=\frac{1}{2}AB.AC=2OA.O'A.\sin\widehat{OAC}.cos\widehat{OAC}\le OA.O'A\left(\sin^2\widehat{OAC}+cos^2\widehat{OAC}\right)=OA.OA'\)
dấu bằng xảy ra khi \(\sin\widehat{OAC}=cos\widehat{OAC}\Rightarrow\widehat{OAC}=45^o\)
từ đó ta xác định được vị trí của B và C