cho tam giác ABC, gọi M là điểm trên cạnh BC sao cho\(\overrightarrow{MB}=2\overrightarrow{MC}\) . Chứng minh: \(\overrightarrow{AM}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
15 tháng 12 2020
Có vẻ không đúng.
Giả sử \(\overrightarrow{AB}+\overrightarrow{MB}+\overrightarrow{MA}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MB}+\left(\overrightarrow{MA}+\overrightarrow{AB}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MB}+\overrightarrow{MB}=\overrightarrow{0}\)
\(\Leftrightarrow2\overrightarrow{MB}=\overrightarrow{0}\)
\(\Leftrightarrow M\equiv B\) (Vô lí)
AH
Akai Haruma
Giáo viên
26 tháng 12 2018
Lời giải:
\(\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}\)
\(=\overrightarrow{MB}+\overrightarrow{BC}+2\overrightarrow{BC}=\overrightarrow{MB}+3\overrightarrow{BC}\)
\(=\overrightarrow{MA}+\overrightarrow{AB}+3(\overrightarrow{BA}+\overrightarrow{AC})\)
\(=-\overrightarrow{AM}+\overrightarrow{AB}-3\overrightarrow{AB}+3\overrightarrow{AC}\)
\(=-\frac{1}{3}\overrightarrow{AB}+\overrightarrow {AB}-3\overrightarrow{AB}+3\overrightarrow{AC}\)
\(=\frac{-7}{3}\overrightarrow{AB}+3\overrightarrow{AC}\)
Ta có đpcm.
20 tháng 8 2022
a;\(\overrightarrow{AB}+2\overrightarrow{AC}\)
\(=\overrightarrow{AM}+\overrightarrow{MB}+2\overrightarrow{AM}+2\overrightarrow{MC}\)
\(=3\overrightarrow{AM}\)
b: \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\)
\(=\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\)
=3vecto MG
24 tháng 9 2023
Tham khảo:
a) M thuộc cạnh BC nên vectơ \(\overrightarrow {MB} \) và \(\overrightarrow {MC} \) ngược hướng với nhau.
Lại có: MB = 3 MC \( \Rightarrow \overrightarrow {MB} = - 3.\overrightarrow {MC} \)
b) Ta có: \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} \)
Mà \(BM = \dfrac{3}{4}BC\) nên \(\overrightarrow {BM} = \dfrac{3}{4}\overrightarrow {BC} \)
\( \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \dfrac{3}{4}\overrightarrow {BC} \)
Lại có: \(\overrightarrow {BC} = \overrightarrow {AC} - \overrightarrow {AB} \) (quy tắc hiệu)
\( \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \dfrac{3}{4}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = \dfrac{1}{4}.\overrightarrow {AB} + \dfrac{3}{4}.\overrightarrow {AC} \)
Vậy \(\overrightarrow {AM} = \dfrac{1}{4}.\overrightarrow {AB} + \dfrac{3}{4}.\overrightarrow {AC} \)
AH
Akai Haruma
Giáo viên
13 tháng 9 2021
Lời giải:
Theo đề ta có: $\overrightarrow{BM}=2\overrightarrow{MC}=-2\overrightarrow{CM}$
$\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}(1)$
$=\overrightarrow{AB}-2\overrightarrow{CM}$
$\overrightarrow{AM}=\overrightarrow{AC}+\overrightarrow{CM}$
$\Rightarrow 2\overrightarrow{AM}=2\overrightarrow{AC}+2\overrightarrow{CM}(2)$
Lấy $(1)+(2)\Rightarrow 3\overrightarrow{AM}=\overrightarrow{AB}+2\overrightarrow{AC}$
$\Rightarrow \overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$
4 tháng 10
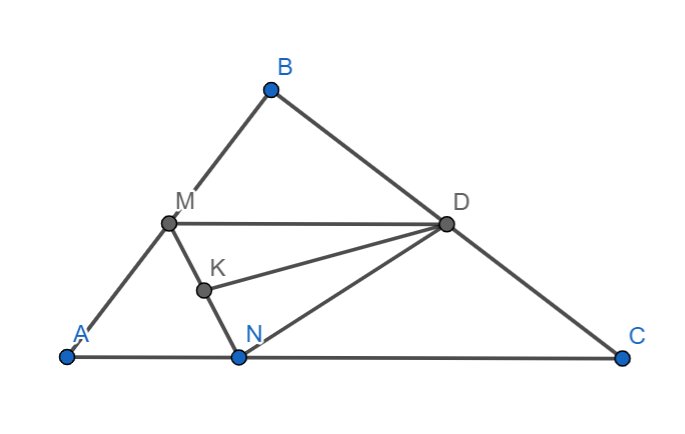
Xét \(\Delta ABC\) có:
\(M\) là trung điểm \(AB\)
\(D\) là trung điểm \(BC\)
\(\Rightarrow\) \(MD\) là đường trung bình của \(\Delta ABC\)
\(\Rightarrow\) \(MD\)\(=\)\(\dfrac{1}{2}AC\) và \(MD\) //\(AC\)
Ta có:
\(\overrightarrow{KD}=\overrightarrow{KM}+\overrightarrow{MD}\)
\(\Rightarrow\overrightarrow{KD}=\dfrac{1}{2}\overrightarrow{NM}+\dfrac{1}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{KD}=\dfrac{1}{2}\overrightarrow{NA}+\dfrac{1}{2}\overrightarrow{AM}+\dfrac{1}{2}\overrightarrow{AC}=\dfrac{1}{6}\overrightarrow{CA}+\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\\ \Rightarrow\overrightarrow{KD}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)
\(=\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}\)
\(=\overrightarrow{AB}+\dfrac{2}{3}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\)