Một vật dao động điều hoà có phương trình dao động là x = 4cos(2 bi t - bi/3) (cm). (x tính bằng cm, t tính bằng s) a) Tính thời gian ngắn nhất đi từ x = 1 cm đến x = -3 cm và thời gian ngắn nhất đi từ x = 2 cm đến x = -2√ cm. b) Tìm thời điểm đầu tiên và lần 10 vật qua x = 2 căn 3cm theo chiều âm? theo chiều dương ? c) Tìm thời điểm lần thứ 2021 vật qua x = 2 căn 3 cm d) Tìm thời điểm lần thứ 2021 vật cách VTCB x = 2 căn 3 cm e) Ở thời điểm t, vật qua x = 2 căn 2 cm cm theo chiều âm thì sau đó và trước đó 7/24 s vật có li độ và vận tốc bằng bao nhiêu? f) Trong khoảng thời gian từ t = 2,25 s đếnn t = 6,5 s vật qua li độ x = 1 cm mấy lần? Mấy lần theo chiều dương ? Mấy lần theo chiều âm ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
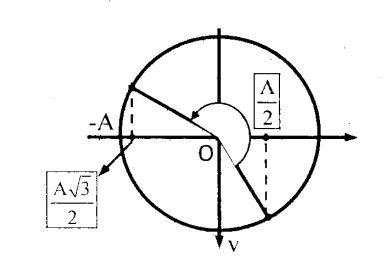
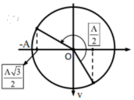
x 1 = 3 = A 2 → x 2 = − 3 2 = − A 3 2
Từ VTLG ta thu được thời gian cần tìm là:
Δ t = T 2 + T 12 → T = 0 , 5 s Δ t = 7 24 s

Đáp án C
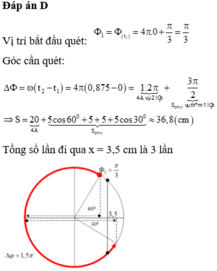
+ Chu kì của dao động T = 1s.
+ Ta tách khoảng thời gian Δt = 1 + 1 3 s , quãng đường vật được trong 1 s luôn là 4A = 32cm.
Quãng đường ngắn nhất đi được trong một pha ba giây còn lại s [ 1 - cos ( ω Δt 2 ) ] [ 1 - cos ( 2 π . 1 6 ) ] min
→ S min

Đáp án A
Vẽ vòng tròn lượng giác ta xác định góc quay tương ứng là 60o+90o+60 = 210o
![]()

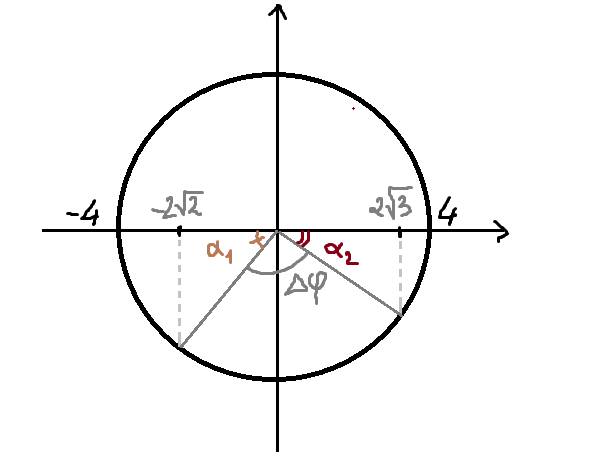
Ta có : \(A=4cm\)
\(cos\alpha_1=\dfrac{-2\sqrt{2}}{4}=-\dfrac{\sqrt{2}}{2}\Rightarrow\alpha_1=\dfrac{3\pi}{4}rad\)
\(cos\alpha_2=\dfrac{2\sqrt{3}}{4}=\dfrac{\sqrt{3}}{2}\Rightarrow\alpha_2=\dfrac{\pi}{6}rad\)
\(\Delta\varphi=\left(\dfrac{\pi}{2}-\dfrac{3\pi}{4}\right)+\left(\dfrac{\pi}{2}-\dfrac{\pi}{6}\right)=\dfrac{\pi}{12}rad\)
Có : \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{\pi}=2s\)
\(\Delta t=\dfrac{\Delta\varphi}{2\pi}.T=\dfrac{\dfrac{\pi}{12}}{2\pi}.2=\dfrac{1}{12}s\)
Vậy ...
Hình ảnh biểu diễn :