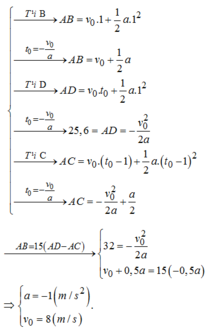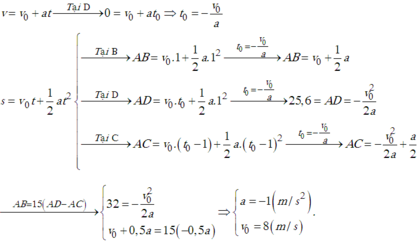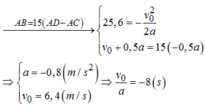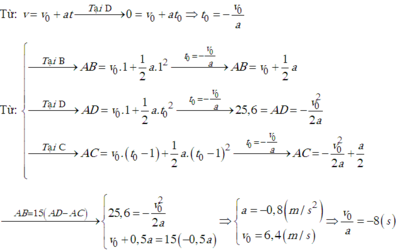Một xe chuyển động chậm dần đều cho đến khi dừng lại. Quãng đường xe đi được trong giây đầu tiên gấp 19 lần quãng đường xe đi được trong giây cuối cùng. Quãng đường đi được trong cả hai giai đoạn này là 100m. Tìm quãng đường ô tô đi được cho đến lúc dừng hẳn.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
30 tháng 7 2019
Ta có
Phương trình quãng đường chuyển động của xe:
S = v 0 t + 1 2 a t 2
Phương trình vận tốc của xe:v=v0+at
Quãng đường xe đi được trong giây đầu tiên:
s 1 = v 0 + 1 2 a
Quãng đường xe đi được đến khi dừng lại:
S = v 0 t + 1 2 a t 2
Quãng đường xe đi được trong(t−1)giây là:
s t − 1 = v 0 ( t − 1 ) + 1 2 a ( t − 1 ) 2
⇒ Quãng đường xe đi được trong giây cuối cùng là:
Δ S = S − S t − 1 = v 0 t + 1 2 a t 2 − v 0 ( t − 1 ) − 1 2 a t - 1 2
= v 0 + a t − 1 2 a
Theo đầu bài ta có: 15 Δ s = s 1
⇔ v 0 + 1 2 a = 15 ( v 0 + a t − 1 2 a )
Lại có: v 0 + a t = v d u n g = 0 m / s
⇒ v 0 + 1 2 a = − 15 a 2 ⇒ v 0 = − 8 a
Áp dụng công thức liên hệ:v2−v02=2as
⇔0−(−8a)2=2.a.96⇒a=−3m/s2
Hợp lực tác dụng vào vật có độ lớn:
F = m a = 1,2.1000.3 = 3600 ( N )
Đáp án: C
27 tháng 11 2021
Vận tốc xe đi trên quãng đường:
\(v=\dfrac{4}{2}=2\)m/s
Thời gian xe đi cả quãng đường:
\(t=\dfrac{225}{2}=112,5s\)
Quãng đường xe đi trong 110,5s:
\(S=110,5\cdot2=221m\)
Quãng đường xe đi trong 2s cuối:
\(S'=225-221=4m\)
15 tháng 7 2019
1)
v0=0
Sgiây thứ 3 = 5m \(\Leftrightarrow S_{giâythứ3}=v_0t+\frac{1}{2}at^2-v_0\left(t-1\right)-\frac{1}{2}a\left(t-1\right)^2=v_0+a\left(t-\frac{1}{2}\right)=0+a\left(3-\frac{1}{2}\right)=\frac{5}{2}a\)
=> \(\frac{5}{2}a=5\)
=> a =2\(m/s^2\)
Quãng đường xe đi được sau 10s là:
t =10s => \(s=v_0t+\frac{1}{2}at^2=\frac{1}{2}.2.10^2=100\left(m\right)\)