cho hàm số f(x)= x3+(a-1)x2+2x+1. để f '(x) >0,với mọi x thuộc R nếu:
a. 1-\(\sqrt{6}\le a\le1+\sqrt{6}\) b. \(1-\sqrt{6}< a< 1+\sqrt{6}\)
c. \(a< 1+\sqrt{6}\) d. \(a\ge1-\sqrt{6}\)
mk cần giải chi tiết ạ( đang cần gấp)
help my! thank nhìu <3 !!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
y = -x3 + (2m – 1)x2 – (2 – m)x – 2
TXĐ: D = R
y' = -3x2 + 2(2m – 1) – 2 + m
Đồ thị hàm số có cực đại và cực tiểu <=> Pt y’ = 0 có hai nghiệm phân biệt
<=> Δ’ = (2m – 1)2 + 3(-2 + m) > 0 <=> 4m2 – m – 5 > 0 <=> m ∈ (-∞; -1) ∪ (5/4; +∞)

- Ta có:
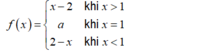
Để f(x) liên tục phải tại điểm x = 1.
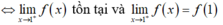
+ Ta có:
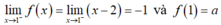
- Vậy điều kiện là a = -1.

- Ta có:
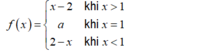
Để f(x) liên tục trái tại điểm x = 1.
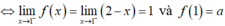
- Vậy điều kiện là a = 1.
Lời giải:
Ta có:
\(f'(x)=3x^2+2(a-1)x+2\)
Theo định lý về dấu của tam thức bậc 2, để \(f'(x)>0\) với mọi \(x\in\mathbb{R}\) thì \(\Delta'=(a-1)^2-6<0\)
\(\Leftrightarrow -\sqrt{6}< a-1< \sqrt{6}\)
\(\Leftrightarrow 1-\sqrt{6}< a< 1+\sqrt{6}\)
Đáp án B