Question

[Nguyễn Vân]

Bài 1: Khử mẫu của biểu thức lấy căn:

a) \(xy\sqrt{\dfrac{x}{y}}\)

b) \(\sqrt{\dfrac{5a^3}{49b}}\left(a\ge0,b>0\right)\)

Bài 2:Trục căn thức ở mẫu:

a) \(\dfrac{\sqrt{3}-3}{1-\sqrt{3}}\)

b) \(\dfrac{5-\sqrt{15}}{\sqrt{3}-\sqrt{5}}\)

c) \(\dfrac{2\sqrt{2}+2}{5\sqrt{2}}\)

Answer 1

[Mysterious Person]

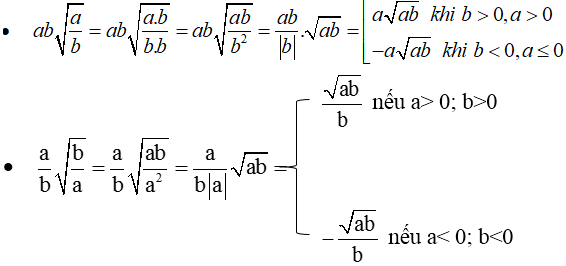
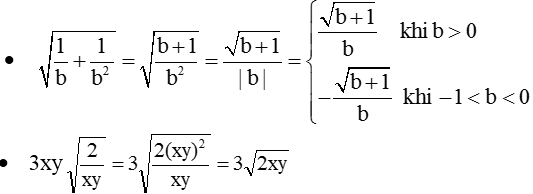
bài 1) a) \(xy\sqrt{\dfrac{x}{y}}=x\sqrt{y}\sqrt{y}\dfrac{\sqrt{x}}{\sqrt{y}}=x\sqrt{x}\sqrt{y}=\left(\sqrt{x}\right)^3\sqrt{y}\)

b) \(\sqrt{\dfrac{5a^3}{49b}}=\dfrac{\sqrt{5a^3}}{\sqrt{49b}}=\dfrac{\sqrt{5a^3}}{7\sqrt{b}}=\dfrac{\sqrt{5a^3}.\sqrt{b}}{7\sqrt{b}.\sqrt{b}}=\dfrac{\sqrt{5a^3b}}{7b}\)

bài 2) a) \(\dfrac{\sqrt{3}-3}{1-\sqrt{3}}=\dfrac{\sqrt{3}\left(1-\sqrt{3}\right)}{1-\sqrt{3}}=\sqrt{3}\)

b) \(\dfrac{5-\sqrt{15}}{\sqrt{3}-\sqrt{5}}=\dfrac{-\sqrt{5}\left(\sqrt{3}-\sqrt{5}\right)}{\sqrt{3}-\sqrt{5}}=-\sqrt{5}\)

c) \(\dfrac{2\sqrt{2}+2}{5\sqrt{2}}=\dfrac{\sqrt{2}\left(2+\sqrt{2}\right)}{5\sqrt{2}}=\dfrac{2+\sqrt{2}}{5}\)