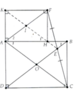
Cho hình chữ nhật ABCD . Nối C với E điểm bất kì trên đường BD . Trên tia đối của EC lấy điểm F sao cho EF = EC . Vẽ FH và FK lần lượt vuông góc với AB và AD .
a) CM tứ giác AHFK là hình chữ nhật
b) CM AF song song BD
c) CM 3 điểm EHK thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 9 2023
a: Xét tứ giác AHFK có
góc AHF=góc AKF=góc KAH=90 độ
=>AHFK là hình chữ nhật
b: Gọi O là giao của AC và BD, I là giao của AF và HK
AHFK là hình chữ nhật
=>I là trung điểm chung của AF và HK
ABCD là hình chữ nhật
=>O là trung điểm chung của AC và BD
Xét ΔAFC có I,O lần lượt là trung điểm của AF,AC
=>IO là đường trung bình
=>IO//FC và IO=FC/2
=>IO//FE và IO=FE
Xét tứ giác IFEO có
IO//FE
IO=FE
=>IFEO là hình bình hành
=>IF//OE
=>AF//BD
CM
30 tháng 5 2018
a) F H A ^ = H A K ^ = A K F ^ = 90 0
Þ AHFK là hình chữ nhật.
b) Gọi là giao điểm của AC và BD. Chứng minh OE là đường trung bình của DACF
Þ AF//OE
Þ AF/BD
c) Gọi I là giao điểm của AF và HK.
Chứng minh
H 1 ^ = A ^ 1 ( H 1 ^ = A 2 ^ = B 1 ^ = A 1 ^ ) ⇒ K H / / A C mà KH đi qua trung điểm I của AF Þ KH đi qua trung điểm của FC.
Mà E là trung điểm của FC Þ K, H, E thẳng hàng
12 tháng 11 2021
a) F H A ^ = H A K ^ = A K F ^ = 90 0
Þ AHFK là hình chữ nhật.
b) Gọi là giao điểm của AC và BD. Chứng minh OE là đường trung bình của DACF
Þ AF//OE
Þ AF/BD
c) Gọi I là giao điểm của AF và HK.
Chứng minh
H 1 ^ = A ^ 1 ( H 1 ^ = A 2 ^ = B 1 ^ = A 1 ^ ) ⇒ K H / / A C mà KH đi qua trung điểm I của AF Þ KH đi qua trung điểm của FC.
Mà E là trung điểm của FC Þ K, H, E thẳng hàng
M
2 tháng 9 2023
a) Để chứng minh BD = 2AO, ta có thể sử dụng định lý Thales và các quy tắc về tỉ lệ đồng dạng. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
b) Để chứng minh I là trung điểm của KH, ta có thể sử dụng các quy tắc về đường thẳng song song và đồng quy. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
c) Để chứng minh tứ giác AIEO là hình bình hành, ta có thể sử dụng các quy tắc về đường chéo và cạnh đối. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
d) Để chứng minh I, K, E thẳng hàng, ta có thể sử dụng các quy tắc về đường thẳng và góc vuông. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
a)Xét tứ giác AHFK có góc AHF=90(gt), góc HAK=90(gt), góc AKF=90(gt)
=> tứ giác AHFK là hcn
b) Gọi O là giao điểm của AC và BD, M là giao điểm của HK và AF
Xét tam giác CAF có CO=OA(gt), CE=EF(gt)
=>OE là đường trung bịnh của tam giác CÀ
=>OE//AF hay BD//AF
Ta có OA=OD(ABCD là hcn)
=> tam giác OAD cân tại O
=>góc OAD=góc ODA
Mà góc ODA=góc FAD(so le trong)
=>góc OAD=góc FAD hay góc CAD=góc MAK(1)
Ta lại có MA=MK(AHFK là hcn)
=>tam giác MAK cân tại M
=>góc MAK= góc MKA(2)
Từ (1) và (2)=>góc CAD=góc MKA hay góc CAD=góc HKA
=>AC//HK(có cặp góc slt bằng nhau)
c)Xét tam giác FAC có FM=MA(AHFK là hcn), FE=EC(gt)
=>ME là đường trung bình của tam giác FAC
=>ME//AC(3)
Mà HK//AC(cmt)(4)
Mặt khác M thuộc AC(5)
Từ (3),(4) và (5)=> H,K,E thẳng hàng
ko có hình khó hiểu quá