mng giúp mk vs !!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 11 2021
a: Xét tứ giác AICK có
AI//CK
AK//CI
Do đó: AICK là hình bình hành
DA
14 tháng 2 2022
1. that
2. that night
3. the day before.
4. my
5. that evening
6. the previous week
7. her
8. there
9. the following day
10. two hours
11. then
14 tháng 2 2022
1.that
2.that night
3.the day before
4.my
5.that night
6.the previous week
7.her 8.there 9 the following day 10.two hours before 11.then
15 tháng 4 2023
a: Xét ΔBDA vuông tại D và ΔBFC vuông tại F có
góc B chung
=>ΔBDA đồng dạng với ΔBFC
=>BD/BF=BA/BC
=>BD*BC=BF*BA và BD/BA=BF/BC
b: Xét ΔBDF và ΔBAC có
BD/BA=BF/BC
góc DBF chung
=>ΔBDF đồng dạng với ΔBAC
c: Xét ΔBDH vuông tại D và ΔBEC vuông tại E có
góc DBH chung
=>ΔBDH đồng dạng với ΔBEC
=>BD/BE=BH/BC
=>BD*BC=BH*BE
Xét ΔCDH vuông tại D và ΔCFB vuông tại F có
góc FCB chung
=>ΔCDH đồng dạng với ΔCFB
=>CD/CF=CH/CB
=>CF*CH=CD*CB
=>BH*BE+CH*CF=BC^2
AH
Akai Haruma
Giáo viên
22 tháng 2 2021
Lời giải:
\(\lim\limits_{x\to 2}\frac{x^2+ax+b}{2x^2-x-6}=\lim\limits_{x\to 2}\frac{x^2+ax+b}{(x-2)(2x+3)}\)
Để giới hạn này là hữu hạn thì $x^2+ax+b\vdots x-2$
$\Rightarrow 2^2+a.2+b=0\Leftrightarrow 2a+b=-4$
Đáp án A.
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 2 2021
\(2x^2-x-6=0\) có 1 nghiệm \(x=2\)
Do đó giới hạn đã cho là hữu hạn khi và chỉ khi \(x^2+ax+b=0\) cũng có 1 nghiệm \(x=2\)
\(\Rightarrow4+2a+b=0\Rightarrow b=-2a-4\)
Vậy:
\(\lim\limits_{x\rightarrow2}\dfrac{x^2+ax-2a-4}{2x^2-x-6}=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+2\right)+a\left(x-2\right)}{\left(x-2\right)\left(2x+3\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+a+2\right)}{\left(x-2\right)\left(2x+3\right)}=\lim\limits_{x\rightarrow2}\dfrac{x+a+2}{2x+3}=\dfrac{a+4}{7}\)
\(\Rightarrow\dfrac{a+4}{7}=\dfrac{3}{2}\Rightarrow a=\dfrac{13}{2}\Rightarrow b=-2a-4=-17\)
\(\Rightarrow2a+b=-4\)
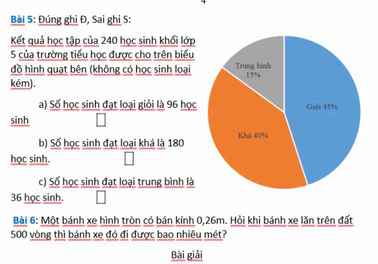
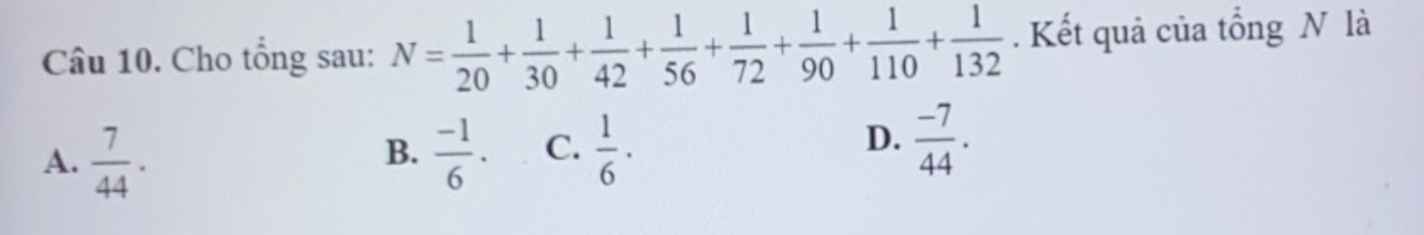
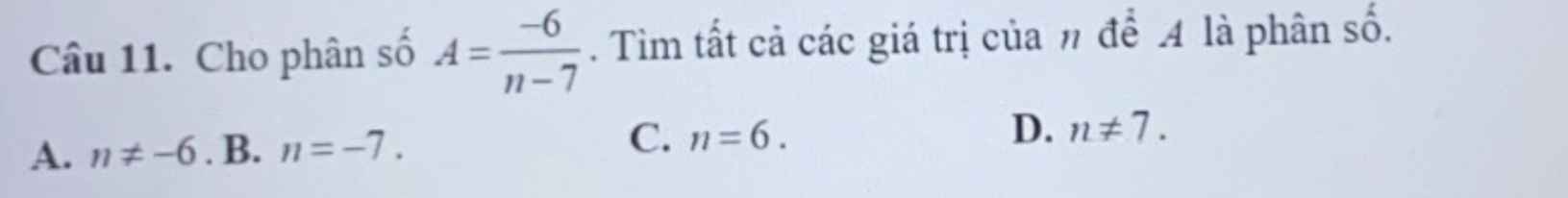
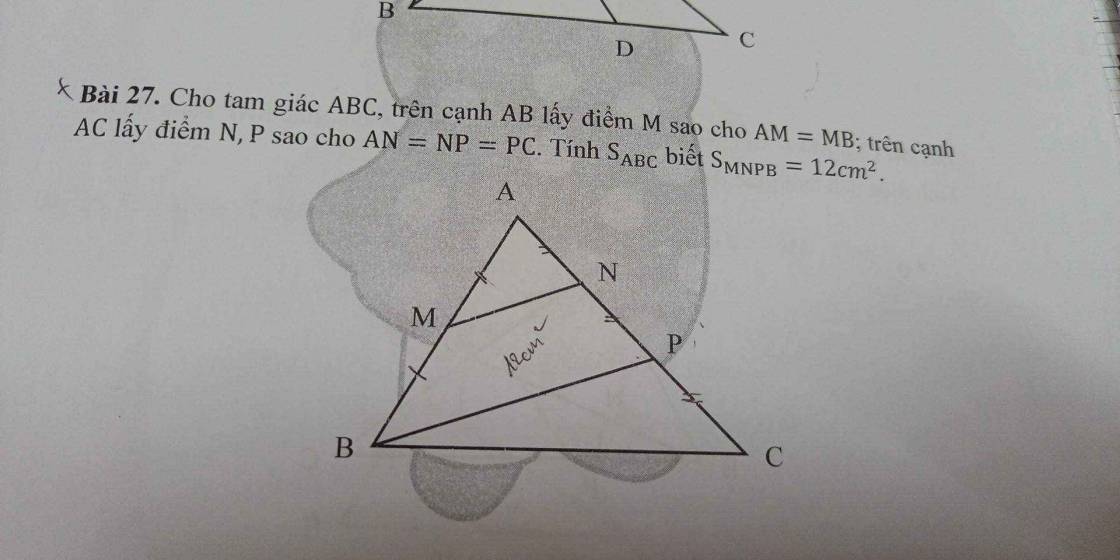
bài cuối nha mng ơi