Cho tam giác ABC, đường cao AA', trực tâm H và biết \(\frac{AH}{A'H}=k\). CMR: tanB.tanC = 1+ k
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 5 2017
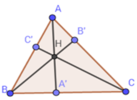
Ta có: SHBC + SHAC + SHAB = SABC
=> S H B C S A B C + S H A C S A B C + S H A B S A B C = 1
ó H A ' . B C A A ' . B C + H B ' . A C B B ' . A C + H C ' . B A C C ' . B A = 1
ó H A ' A A ' + H B ' B B ' + H C ' C C ' = 1 (đpcm)
Đáp án cần chọn là: A
VN
0
góc B = góc H1 vì cùng phụ với góc BAA' nên góc B= góc H2
tanB.tanC = tanH.tanC = \(\dfrac{A'C}{A'H}.\dfrac{AA'}{A'C}=\dfrac{AA'}{A'H}=\dfrac{A'H+AH}{A'H}=1+\dfrac{AH}{A'H}=1+k\)