Trong các số sau, số nào có căn bậc hai? Tìm căn bậc hai của chúng (nếu có).
0; -16; 32 + 42; 52 - 42; (-5)2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các số có căn bậc hai:
a = 0 c = 1 d = 16 + 9
e = 32 + 42 h = (2-11)2 i = (-5)2
l = √16 m = 34 n = 52 - 32
Căn bậc hai không âm của các số đó là:
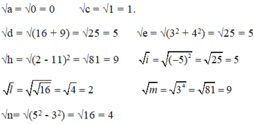

Ta có: √ 121 = 11 v ì 11 > 0 v à 11 2 = 121 n ê n
Căn bậc hai số học của 121 là 11. Căn bậc hai của 121 là 11 và – 11.
Tương tự:
Căn bậc hai số học của 144 là 12. Căn bậc hai của 144 là 12 và -12.
Căn bậc hai số học của 169 là 13. Căn bậc hai của 169 là 13 và -13.
Căn bậc hai số học của 225 là 15. Căn bậc hai của 225 là 15 và -15.
Căn bậc hai số học của 256 là 16. Căn bậc hai của 256 là 16 và -16.
Căn bậc hai số học của 324 là 18. Căn bậc hai của 324 là 18 và -18.
Căn bậc hai số học của 361 là 19. Căn bậc hai của 361 là 19 và -19.
Căn bậc hai số học của 400 là 20. Căn bậc hai của 400 là 20 và -20.

Ta có: √121 = 11 vì 11 > 0 và 112 = 121 nên
Căn bậc hai số học của 121 là 11. Căn bậc hai của 121 là 11 và – 11.
Tương tự:
Căn bậc hai số học của 144 là 12. Căn bậc hai của 144 là 12 và -12.
Căn bậc hai số học của 169 là 13. Căn bậc hai của 169 là 13 và -13.
Căn bậc hai số học của 225 là 15. Căn bậc hai của 225 là 15 và -15.
Căn bậc hai số học của 256 là 16. Căn bậc hai của 256 là 16 và -16.
Căn bậc hai số học của 324 là 18. Căn bậc hai của 324 là 18 và -18.
Căn bậc hai số học của 361 là 19. Căn bậc hai của 361 là 19 và -19.
Căn bậc hai số học của 400 là 20. Căn bậc hai của 400 là 20 và -20.

\(\sqrt{121}=11\); \(\sqrt{144}=12\)
\(\sqrt{169}=13\); \(\sqrt{225}=15\);
\(\sqrt{256}=16\); \(\sqrt{324}=18\);
\(\sqrt{361}=19\); \(\sqrt{400}=20\)
Để tìm căn bậc hai của các số này, bạn có thể sử dụng tính toán hoặc dùng máy tính. Dưới đây là căn bậc hai của mỗi số:
1. Căn bậc hai của 121 là √121 = 11.
2. Căn bậc hai của 144 là √144 = 12.
3. Căn bậc hai của 169 là √169 = 13.
4. Căn bậc hai của 225 là √225 = 15.
5. Căn bậc hai của 256 là √256 = 16.
6. Căn bậc hai của 324 là √324 = 18.
7. Căn bậc hai của 361 là √361 = 19.
8. Căn bậc hai của 400 là √400 = 20.
Vậy căn bậc hai của các số đó lần lượt là: 11, 12, 13, 15, 16, 18, 19, và 20.

Gọi số đó là 10a+b (a, b nguyên; 0<a<10; 0<=b<10)
Khi đó: √(10a+b) = a + √b
Để √(10a+b) nguyên thì √b nguyên <=> b = 1 hoặc 4 hoặc 9
Bình phương hai vế => a^2 - (10-2√b)a = 0
<=> a(a-10+2√b) = 0
a = 0 (loại)
=> a-10+2√b = 0 <=> a = 10-2√b
+) b = 1 <=> a = 8 => 81 thỏa mãn
+) b = 4 <=> a = 6 => 64 thỏa mãn
+) b = 9 <=> a = 4 => 49 thỏa mãn
ok bạn nhá

Căn bậc hai số học của 17 là \(\sqrt{17}\)
Căn bậc hai của 17 là \(\pm\sqrt{17}\)
Căn bậc hai số học của 19 là \(\sqrt{19}\)
Căn bậc hai của 19 là \(\pm\sqrt{19}\)
Một số không âm mới có căn bậc hai.
Vậy trong các số đã cho, các số có căn bậc hai là \(0;3^2+4^2;5^2-4^2;\left(-5\right)^2\)
Căn bậc hai của chúng là:
- Với số \(0\): \(\sqrt{0}=0\)
- Với số \(3^2+4^2=9+16=25=5^2\)
nên \(\sqrt{3^2+4^2}=5;-\sqrt{3^2+4^2}=-5\)
- Với số \(5^2-4^2=25-16=9=3^2\)
nên \(\sqrt{5^2-4^2}=3;-\sqrt{5^2-4^2}=-3\)
- Với số \(\left(-5\right)^2=25=5^2\)
nên \(\sqrt{\left(-5\right)^2}=5;-\sqrt{\left(-5\right)^2}=-5\)