Cho nửa đường tròn (O), đương kính AB, các tia tiếp tuyến Ax và By. Tiếp tuyến của nửa đường tròn tạo M cắt Ax tại C, cắt By tại D. Gọi giao điểm của AD với BC là N, MN cắt AB ở I. Chứng minh
a) CD = AC + BD
b) MN\(\\\)//AC
c) N là trung điểm của MI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 1 2021
a) Xét (O) có
CM là tiếp tuyến có M là tiếp điểm(gt)
CA là tiếp tuyến có A là tiếp điểm(gt)
Do đó: CM=CA(Tính chất hai tiếp tuyến cắt nhau)
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm(gt)
DB là tiếp tuyến có B là tiếp điểm(gt)
Do đó: DB=DM(Tính chất hai tiếp tuyến cắt nhau)
Ta có: CD=CM+DM(M nằm giữa C và D)
mà CM=CA(cmt)
và DM=DB(cmt)
nên CD=CA+DB
3 tháng 10 2021
a) Xét tứ giác AOMC có
ˆCAOCAO^ và ˆCMOCMO^ là hai góc đối
ˆCAO+ˆCMO=1800(900+900=1800)CAO^+CMO^=1800(900+900=1800)
Do đó: AOMC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Ta có: AOMC là tứ giác nội tiếp(cmt)
nên ˆMAO=ˆOCMMAO^=OCM^(hai góc cùng nhìn cạnh OM)
hay ˆMAB=ˆOCDMAB^=OCD^
Xét (O) có
CM là tiếp tuyến có M là tiếp điểm(Gt)
CA là tiếp tuyến có A là tiếp điểm(Gt)
Do đó: OC là tia phân giác của ˆAOMAOM^(Tính chất hai tiếp tuyến cắt nhau)
⇔ˆAOM=2⋅ˆCOM⇔AOM^=2⋅COM^
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm(gt)
DB là tiếp tuyến có B là tiếp điểm(gt)
Do đó: OD là tia phân giác của ˆMOBMOB^(Tính chất hai tiếp tuyến cắt nhau)
⇔ˆBOM=2⋅ˆMOD⇔BOM^=2⋅MOD^
Ta có: ˆAOM+ˆBOM=1800AOM^+BOM^=1800(hai góc kề bù)
mà ˆAOM=2⋅ˆCOMAOM^=2⋅COM^(cmt)
và ˆBOM=2⋅ˆMODBOM^=2⋅MOD^(cmt)
nên 2⋅ˆCOM+2⋅ˆMOD=18002⋅COM^+2⋅MOD^=1800
⇔ˆCOM+ˆMOD=900⇔COM^+MOD^=900
mà ˆCOM+ˆMOD=ˆCODCOM^+MOD^=COD^(tia OM nằm giữa hai tia OC,OD)
nên ˆCOD=900COD^=900
Xét ΔCOD có ˆCOD=900COD^=900(cmt)
nên ΔCOD vuông tại O(Định nghĩa tam giác vuông)
Xét (O) có
ΔMAB nội tiếp đường tròn(M,A,B∈(O))
AB là đường kính(gt)
Do đó: ΔMAB vuông tại M(Định lí)
Xét ΔAMB vuông tại M và ΔCOD vuông tại O có
ˆMAB=ˆOCDMAB^=OCD^(cmt)
Do đó: ΔAMB∼ΔCOD(g-g)
⇔AMCO=BMDOAMCO=BMDO(Các cặp cạnh tương ứng tỉ lệ)
hay AM⋅OD=BM⋅OCAM⋅OD=BM⋅OC(đpcm)
14 tháng 3 2023
a: Xét (O) co
CM,CA là tiếp tuyên
=>CM=CA
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB
CD=CM+MD
=>CD=CA+BD
b: Xet ΔACN và ΔDBN có
góc NAC=góc NDB
góc ANC=góc DNB
=>ΔACN đồng dạng vơi ΔDBN
=>AC/BD=AN/DN
=>CN/MD=AN/ND
=>MN/AC
CM
20 tháng 5 2017
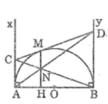
Ax ⊥ AB
By ⊥ AB
Suy ra: Ax // By hay AC // BD
Trong tam giác BND, ta có AC // BD
Suy ra: ND/NA = BD/AC (hệ quả định lí Ta-lét) (1)
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = CM và BD = DM (2)
Từ (1) và (2) suy ra: ND/NA = MD/MC
Trong tam giác ACD, ta có: ND/NA = MD/MC
Suy ra: MN // AC (theo định lí đảo định lí Ta-lét)
Mà: AC ⊥ AB (vì Ax ⊥ AB)
Suy ra: MN ⊥ AB
HH
16 tháng 7 2020
Ax \(\perp\) AB
By \(\perp\) AB
Suy ra: Ax // By hay AC // BD
Trong tam giác BND, ta có AC // BD
Suy ra: \(\frac{ND}{NA}=\frac{BD}{AC}\)(hệ quả định lí Ta-lét) (1)
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = CM và BD = DM (2)
Từ (1) và (2) suy ra: \(\frac{ND}{NA}=\frac{MD}{MC}\)
Trong tam giác ACD, ta có: \(\frac{ND}{NA}=\frac{MD}{MC}\)
Suy ra: MN // AC (theo định lí đảo định lí Ta-lét)
Mà: AC \(\perp\) AB (vì Ax \(\perp\) AB)
Suy ra: MN \(\perp\) AB
b. Trong tam giác ACD, ta có: MN // AC
Suy ra: \(\frac{MN}{AC}=\frac{DN}{DA}\) (hệ quả định lí Ta-lét) (3)
Trong tam giác ABC, ta có: MH // AC (vì M, N, H thẳng hàng)
Suy ra: \(\frac{HN}{AC}=\frac{BN}{BC}\) (hệ quả định lí Ta-lét) (4)
Trong tam giác BDN, ta có: AC // BD
Suy ra: \(\frac{ND}{NA}=\frac{BN}{NC}\) (hệ quả định lí Ta-lét)
\(\Rightarrow\frac{ND}{\left(DN+NA\right)}=\frac{BN}{\left(BN+NC\right)}\Leftrightarrow\frac{ND}{DA}=\frac{BN}{BC}\left(5\right)\)
Từ (3), (4) và (5) suy ra: MN/AC = HN/AC => MN = HN
CM
9 tháng 10 2017
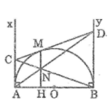
Trong tam giác ACD, ta có: MN // AC
Suy ra: MN/AC = DN/DA (hệ quả định lí Ta-lét) (3)
Trong tam giác ABC, ta có: MH // AC (vì M, N, H thẳng hàng)
Suy ra: HN/AC = BN/BC (hệ quả định lí Ta-lét) (4)
Trong tam giác BDN, ta có: AC // BD
Suy ra: ND/NA = BN/NC (hệ quả định lí Ta-lét)
⇒ ND/(DN + NA) = BN/(BN + NC) ⇔ ND/DA = BN/BC (5)
Từ (3), (4) và (5) suy ra: MN/AC = HN/AC ⇒ MN = HN
CH
Cô Hoàng Huyền
Admin
VIP
7 tháng 6 2016
Cô hướng dẫn nhé nguyen van vu :)
a. Ta có góc COD = COM + MOD = \(\frac{AOM}{2}+\frac{BOM}{2}=\frac{180}{2}=90^o\)
b. Dễ thấy E là trung điểm CD, O là trung điểm AB nên OE song song AC. Vậy OE vuông góc AB.
c. Gọi MH là đường thẳng vuông góc AB, Ta chứng minh BC, AD đều cắt MH tại trung điểm của nó.
Gọi I là giao của AM và BD. Đầu tiên chứng minh ID = DB. Thật vậy, góc MID=IMD (Cùng bằng cung AM/2)
nên ID =MD, mà MD=DB nên ID=DB.
Gọi K là giao của MH và AD.
Theo Talet , \(\frac{MK}{DI}=\frac{AK}{AD}=\frac{KH}{BD}\Rightarrow MK=KH\)
Tương tự giao điểm của BC với MH cũng là trung điểm MH.
Tóm lại N trùng K hay MN vuông góc AB.
a: Xét (O) co
CM,CA là tiếp tuyên
=>CM=CA
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB
CD=CM+MD
=>CD=CA+BD
b: Xet ΔACN và ΔDBN có
góc NAC=góc NDB
góc ANC=góc DNB
=>ΔACN đồng dạng vơi ΔDBN
=>AC/BD=AN/DN
=>CN/MD=AN/ND
=>MN/AC
c: MN//AC; AC vuông góc AB
=>MN vuông góc AB
Xét ΔBIN vuông tại I và ΔBAC vuông tại A có
góc IBN chung
=>ΔBIN đồng dạng vơi ΔBAC
=>NI/AC=BN/BC
MN//AC
=>MN/AC=ND/AD
=>AN/ND=NC/NB
=>ND/AD=BN/BC
=>MN/AC=NI/AC
=>NM=NI
=>N là trung điểm của MI
a: Xét (O) co
CM,CA là tiếp tuyên
=>CM=CA
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB
CD=CM+MD
=>CD=CA+BD
b: Xet ΔACN và ΔDBN có
góc NAC=góc NDB
góc ANC=góc DNB
=>ΔACN đồng dạng vơi ΔDBN
=>AC/BD=AN/DN
=>CN/MD=AN/ND
=>MN/AC
c: MN//AC; AC vuông góc AB
=>MN vuông góc AB
Xét ΔBIN vuông tại I và ΔBAC vuông tại A có
góc IBN chung
=>ΔBIN đồng dạng vơi ΔBAC
=>NI/AC=BN/BC
MN//AC
=>MN/AC=ND/AD
=>AN/ND=NC/NB
=>ND/AD=BN/BC
=>MN/AC=NI/AC
=>NM=NI
=>N là trung điểm của MI