1.Cho đoạn thẳng AB=a, M là trung điểm AB. Vẽ về 1 phía của AB các tia Ax, By vuông góc AB. Lấy C trên tia Ax và D trên tia By sao cho góc CMD=90độ.
A, CM: Tính tích AC.BD theo a.
B. CM: Tam giác MAC và tam giác BMC đồng dạng.
2. Cho tam giác ABC, có 3 góc đều nhọn. Các đường cao BD và CE cắt nhau tại H. Kẻ cuông góc BC,CK.(K thuộc BC).
A. CM: BH.BD=BK.BC.
B. CM: CH.CE=CK.CB.
C. CM: BH.BD+CH.CE+BC²

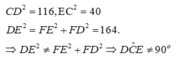
Bài 2:
a: Xét ΔBKH vuông tại K và ΔBDC vuông tại D có
góc KBH chung
Do đo: ΔBKH\(\sim\)ΔBDC
Suy ra: BK/BD=BH/BC
hay \(BK\cdot BC=BH\cdot BD\)
b: Xét ΔCKH vuông tại K và ΔCEB vuông tại E có
góc ECB chung
Do đó: ΔCKH\(\sim\)ΔCEB
Suy ra: CK/CE=CH/CB
hay \(CK\cdot CB=CH\cdot CE\)
c: \(BH\cdot BD+CH\cdot CE\)
\(=BK\cdot BC+CK\cdot BC\)
\(=BC^2\)